题目内容
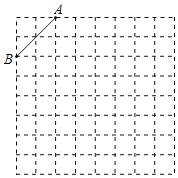
【题目】如图是8×8的正方形网格,请在所给网格中按下列要求操作:
(1)在网格中建立平面直角坐标系,使点A的坐标为(﹣2,4),点B的坐标为(﹣4,2);
(2)在第二象限内的格点上画一点C,连接AC,BC,使△BC成为以AB为底的等腰三角形,且腰长是无理数.
①此时点C的坐标为 ,△ABC的周长为 (结果保留根号);
②画出△ABC关于y轴对称的△A′B'C′(点A,B,C的对应点分别A',B',C′),并写出A′,B′,C′的坐标.
【答案】(1)见解析;(2)①(﹣1,1),2![]() +2
+2![]() ;②作图见解析,A′(2,4),B′(4,2),C′(1,1).
;②作图见解析,A′(2,4),B′(4,2),C′(1,1).
【解析】
(1)根据A点的坐标,即可确定坐标系的位置;
(2)①在第二象限内的格点上画一点C,使点C与线段AB组成一个以AB为底的等腰三角形,则C一定在AB的中垂线上,通过作图即可确定C的位置;根据勾股定理即可求得三角形的周长;②依据轴对称的性质,即可得到△ABC关于y轴对称的△A'B'C',即可得到A′,B′,C′的坐标.
解:(1)如图,平面直角坐标系如下:

(2)①如图,C点坐标为(﹣1,1),
AB=![]() =2
=2![]() ,BC=AC=
,BC=AC=![]() =
=![]() ,
,
所以△ABC的周长是2![]() +2
+2![]() .
.
故答案为(﹣1,1),2![]() +2
+2![]() ;
;
②如图,△A'B'C'即为所求,A′(2,4),B′(4,2),C′(1,1).

练习册系列答案
相关题目