题目内容
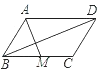
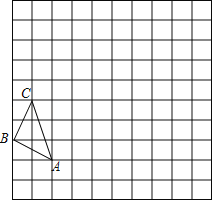
【题目】已知：如图，四边形
的对角线
、
相交于点
，
.
（1）求证：
；
（2）设
的面积为
，
，求证：S四边形ABCD
.
【答案】（1）证明见解析；（2）证明见解析
【解析】
（1）由S△AOD=S△BOC易得S△ADB=S△ACB，根据三角形面积公式得到点D和点C到AB的距离相等，则CD∥AB，于是可判断△DOC∽△BOA，然后利用相似比即可得到结论；
（2）利用相似三角形的性质可得结论．
（1）∵S△AOD=S△BOC，
∴S△AOD+S△AOB=S△BOC+S△AOB，即S△ADB=S△ACB，
∴CD∥AB，
∴△DOC∽△BOA，
∴
；
（2）∵△DOC∽△BOA
∴
＝k，
2=k2，
∴DO=kOB，CO=kAO，S△COD=k2S，
∴S△AOD=kS△OAB=kS，S△COB=kS△OAB=kS，
∴S四边形ABCD=S+kS+kS+k2S=（k+1）2S．
练习册系列答案
相关题目
