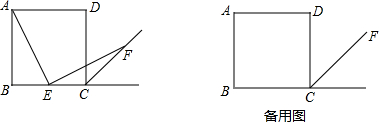题目内容
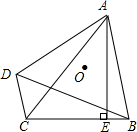 如图,四边形ABCD的对角线CA平分∠BCD且AD=AB,AE⊥CB于E,点O为四边形ABCD的外接圆的圆心,下列结论:(1)OA⊥DB;(2)CD+CB=2CE;(3)∠CBA-∠DAC=∠ACB;(4)若∠DAB=90°,则CD+CB=
如图,四边形ABCD的对角线CA平分∠BCD且AD=AB,AE⊥CB于E,点O为四边形ABCD的外接圆的圆心,下列结论:(1)OA⊥DB;(2)CD+CB=2CE;(3)∠CBA-∠DAC=∠ACB;(4)若∠DAB=90°,则CD+CB= CA.其中正确的结论是
CA.其中正确的结论是
- A.(1)(3)(4)
- B.(1)(2)(4)
- C.(2)(3)(4)
- D.(1)(2)(3)
D
分析:(1)易知:OA=OB=OD(都是⊙O的半径),因此点O是△ABD的外心,因此O点在BD的垂直平分线上,由于△ABD是等腰三角形,因此OA⊥BD,可证得(1)正确;
(2)本题可通过构建等腰三角形求解;延长CB至F,使BF=CD,连接AF;证△ABF≌△ADC;可的BF=CD,CF=2CE,即可证得(2)的结论也正确;
(3)由(2)可得:∠BAF=∠DAC,因此∠CBA-∠BAF=∠F=∠ACB,可证得(3)的结论正确;
(4)若∠DAB=90°,那么△DAB和△ACF都是等腰直角三角形,那么CF= AC,即CB+CD=
AC,即CB+CD= AC,显然(4)的结论是错误的.
AC,显然(4)的结论是错误的.
解答: 解:(1)中,根据点O为四边形ABCD的外接圆的圆心,则OA=OB=OD,
解:(1)中,根据点O为四边形ABCD的外接圆的圆心,则OA=OB=OD,
即点O也是三角形ABD的外心,
因此O是该三角形三边垂直平分线的交点,
又AB=AD,则OA⊥BD;故(1)正确;
(2)中,延长CB至F,使BF=CD,连接AF,
根据圆内接四边形的对角互补,则∠ADC+∠ABC=180°,
又∠ABC+∠ABF=180°,∴∠ABF=∠ADC,
又AB=AD,BF=CD;∴△ABF≌△ADC,
∴AF=AC,又AE⊥CF,∴CE=EF,
即CD+CB=2CE,故(2)正确;
(3)中,根据(2)中的方法,得∠DAC=∠BAF,
∴∠CBA-∠DAC=∠CBA-∠BAF=∠AFC=∠ACB;因此(3)正确;
(4)中,若∠DAB=90°,则∠DCB=90°,则∠ACE=45°,
得到△ACE是等腰直角三角形,根据(2)中的做法,则CD+CB=2CE= CA,故(4)错误.
CA,故(4)错误.
因此正确的结论有:(1)(2)(3),故选D.
点评:此题综合考查了圆内接四边形的性质,能够构造全等三角形,掌握全等三角形的判定和性质.
分析:(1)易知:OA=OB=OD(都是⊙O的半径),因此点O是△ABD的外心,因此O点在BD的垂直平分线上,由于△ABD是等腰三角形,因此OA⊥BD,可证得(1)正确;
(2)本题可通过构建等腰三角形求解;延长CB至F,使BF=CD,连接AF;证△ABF≌△ADC;可的BF=CD,CF=2CE,即可证得(2)的结论也正确;
(3)由(2)可得:∠BAF=∠DAC,因此∠CBA-∠BAF=∠F=∠ACB,可证得(3)的结论正确;
(4)若∠DAB=90°,那么△DAB和△ACF都是等腰直角三角形,那么CF=
 AC,即CB+CD=
AC,即CB+CD= AC,显然(4)的结论是错误的.
AC,显然(4)的结论是错误的.解答:
 解:(1)中,根据点O为四边形ABCD的外接圆的圆心,则OA=OB=OD,
解:(1)中,根据点O为四边形ABCD的外接圆的圆心,则OA=OB=OD,即点O也是三角形ABD的外心,
因此O是该三角形三边垂直平分线的交点,
又AB=AD,则OA⊥BD;故(1)正确;
(2)中,延长CB至F,使BF=CD,连接AF,
根据圆内接四边形的对角互补,则∠ADC+∠ABC=180°,
又∠ABC+∠ABF=180°,∴∠ABF=∠ADC,
又AB=AD,BF=CD;∴△ABF≌△ADC,
∴AF=AC,又AE⊥CF,∴CE=EF,
即CD+CB=2CE,故(2)正确;
(3)中,根据(2)中的方法,得∠DAC=∠BAF,
∴∠CBA-∠DAC=∠CBA-∠BAF=∠AFC=∠ACB;因此(3)正确;
(4)中,若∠DAB=90°,则∠DCB=90°,则∠ACE=45°,
得到△ACE是等腰直角三角形,根据(2)中的做法,则CD+CB=2CE=
 CA,故(4)错误.
CA,故(4)错误.因此正确的结论有:(1)(2)(3),故选D.
点评:此题综合考查了圆内接四边形的性质,能够构造全等三角形,掌握全等三角形的判定和性质.

练习册系列答案
相关题目
 如图,四边形ABCD的对角线AC与BD互相垂直平分于点O,设AC=2a,BD=2b,请推导这个四边形的性质.(至少3条)
如图,四边形ABCD的对角线AC与BD互相垂直平分于点O,设AC=2a,BD=2b,请推导这个四边形的性质.(至少3条) 如图,四边形ABCD的对角线AC、BD交于点P,过点P作直线交AD于点E,交BC于点F.若PE=PF,且AP+AE=CP+CF.
如图,四边形ABCD的对角线AC、BD交于点P,过点P作直线交AD于点E,交BC于点F.若PE=PF,且AP+AE=CP+CF.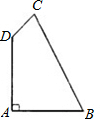 如图,四边形ABCD,AB=AD=2,BC=3,CD=1,∠A=90°,求∠ADC的度数.
如图,四边形ABCD,AB=AD=2,BC=3,CD=1,∠A=90°,求∠ADC的度数.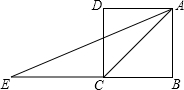 如图,四边形ABCD为正方形,E是BC的延长线上的一点,且AC=CE,求∠DAE的度数.
如图,四边形ABCD为正方形,E是BC的延长线上的一点,且AC=CE,求∠DAE的度数.