题目内容
【题目】某校组织学生开展义务植树活动,在活动结束后随机调查了40名学生每人植树的棵数,根据调查获取的样本数据,制作了条形统计图和扇形统计图.请根据相关信息,解答下列问题:
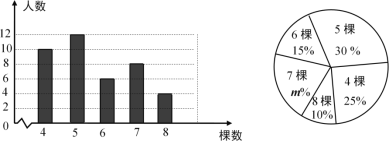
(1)扇形图中![]() 的值是_________;
的值是_________;
(2)求随机调查的40名学生每人植树棵数这组数据的平均数、众数和中位数;
(3)若本次活动九年级共有300名学生参加,估计植树超过6棵(不含6棵)的学生约有多少人.
【答案】(1)20;(2)平均数是5.6;众数是5;中位数是![]() ;(3)植树超过6棵(不含6棵)约有90人
;(3)植树超过6棵(不含6棵)约有90人
【解析】
(1)根据扇形统计图中的数据,即可得到m的值;
(2)根据条形统计图中的数据,即可得到这组数据的平均数、众数和中位数;
(3)根据扇形统计图中的数据,即可计算出植树超过6棵(不含6棵)的学生约有多少人.
解:(1))m%=1-25%-30%-15%-10%=20%,
即m的值是20.
故答案为:20;
(2)∵![]() ,
,
∴平均数是5.6;
∵5出现了12次,出现次数最多,
∴众数是5;
∵将这40个数据按从小到大顺序排列,中间的两个数都是5,
∴中位数是![]() .
.
(3)∵![]() ,
,
∴植树超过6棵(不含6棵)约有90人.

 优加精卷系列答案
优加精卷系列答案【题目】甲、乙两个芭蕾舞团演员的身高(单位:cm)如下表:
甲 | 164 | 164 | 165 | 165 | 166 | 166 | 167 | 167 |
乙 | 163 | 163 | 165 | 165 | 166 | 166 | 168 | 168 |
两组芭蕾舞团演员身高的方差较小的是______.(填“甲”或“乙”)
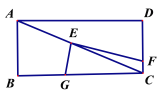
【题目】如图,在△ABC中,AE平分∠BAC交BC于点E,D是AB边上一动点,连接CD交AE于点P,连接BP.已知AB =6cm,设B,D两点间的距离为xcm,B,P两点间的距离为y1cm,A,P两点间的距离为y2cm.
小明根据学习函数的经验,分别对函数y1,y2随自变量x的变化而变化的规律进行了探究.
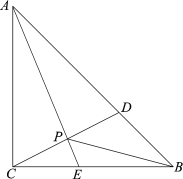
下面是小明的探究过程,请补充完整:
(1)按照下表中自变量x的值进行取点、画图、测量,分别得到了y1,![]() 与x的几组对应值:
与x的几组对应值:
x/cm | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
y1/cm | 2.49 | 2.64 | 2.88 | 3.25 | 3.80 | 4.65 | 6.00 |
y2/cm | 4.59 | 4.24 | 3.80 | 3.25 | 2.51 | 0.00 |
(2)在同一平面直角坐标系xOy中,描出补全后的表中各组数值所对应的点(x,y1),(x,![]() ),并画出函数y1,
),并画出函数y1,![]() 的图象;
的图象;

(3)结合函数图象,回答下列问题:
①当AP=2BD时,AP的长度约为 cm;
②当BP平分∠ABC时,BD的长度约为 cm.