题目内容
【题目】证明定理：三角形三条边的垂直平分线相交于一点，并且这一点到三个顶点的距离相等．
已知：如图，在△ABC中，分别作AB边、BC边的垂直平分线，两线相交于点P，分别交AB边、BC边于点E、F．
求证：AB、BC、AC的垂直平分线相交于点P
证明：∵点P是AB边垂直平线上的一点，
∴=（）．
同理可得，PB= ．
∴=（等量代换）．
∴（到一条线段两个端点距离相等的点，在这条线段的）
∴AB、BC、AC的垂直平分线相交于点P，且 ． 
【答案】PB；PA；垂直平分线上任意一点，到线段两端点的距离相等；PC；PA；PC；点P在AC的垂直平分线上；垂直平分线上；PA=PB=PC
【解析】证明：∵点P是AB边垂直平线上的一点，
∴PB=PA （垂直平分线上任意一点，到线段两端点的距离相等）．
同理可得，PB=PC．
∴PA=PC（等量代换）．
∴点P是AC边垂直平线上的一点（到一条线段两个端点距离相等的点，在这条线段的垂直平分线上），
∴AB、BC、AC的垂直平分线相交于点P，且PA=PB=PC．
故答案为：PB；PA；垂直平分线上任意一点，到线段两端点的距离相等；PC；PA；PC；点P在AC的垂直平分线上，垂直平分线上；PA=PB=PC．
根据线段垂直平分线的性质可得出PB=PA，同理可得出PA=PC，由此即可得出PA=PC，再根据线段垂直平分线的性质可得出点P是AC边垂直平线上的一点，从而证出结论．
练习册系列答案
相关题目
【题目】下面的图形是由边长为1的正方形按照某种规律排列而组成的．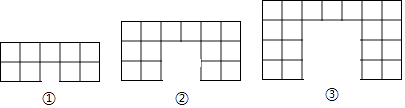
（1）观察图形，填写下表：
图形个数（n） | ① | ② | ③ |
正方形的个数 | 9 | ||
图形的周长 | 16 |
（2）推测第n个图形中，正方形的个数为 ， 周长为（都用含n的代数式表示）．
（3）写出第2016个图形的周长．