题目内容
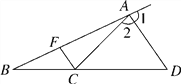
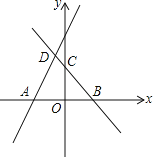
【题目】如图,![]() 是等边三角形,
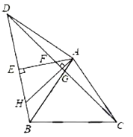
是等边三角形,![]() 是等腰直角三角形,∠BAD=90°,AE⊥BD于点E.连CD分别交AE,AB于点F,G,过点A做AH⊥CD交BD于点H,则下列结论:①∠ADC=15°;②AF=AG;③AH=DF;④△ADF≌△BAH;⑤DF=2EH.其中正确结论的个数为( )
是等腰直角三角形,∠BAD=90°,AE⊥BD于点E.连CD分别交AE,AB于点F,G,过点A做AH⊥CD交BD于点H,则下列结论:①∠ADC=15°;②AF=AG;③AH=DF;④△ADF≌△BAH;⑤DF=2EH.其中正确结论的个数为( )
A. 5B. 4C. 3D. 2
【答案】B
【解析】
①根据△ABC为等边三角形,△ABD为等腰直角三角形,可以得出各角的度数以及DA=AC,即可作出判断;②分别求出∠AFG和∠AGD的度数,即可作出判断;④根据三角形内角和定理求出∠HAB的度数,求证![]() ,利用AAS即可证出两个三角形全等;③根据④证出的全等即可作出判断;⑤证明∠EAH=30°,即可得到AH=2EH,又由③可知
,利用AAS即可证出两个三角形全等;③根据④证出的全等即可作出判断;⑤证明∠EAH=30°,即可得到AH=2EH,又由③可知![]() ,即可作出判断.
,即可作出判断.
①正确:∵![]() 是等边三角形,
是等边三角形,
∴![]() ,∴
,∴![]() .
.
∵![]() 是等腰直角三角形,∴
是等腰直角三角形,∴![]() .
.
又∵![]() ,∴
,∴![]() ,
,
∴![]() ,∴
,∴![]() ;
;
②错误:∵∠EDF=∠ADB-∠ADC=30°
∴∠DFE=90°-∠EDF=90°-30°=60°=∠AFG
∵∠AGD=90°-∠ADG=90°-15°=75°
∠AFG≠∠AGD
∴AF≠AG
③,④正确,由题意可得![]() ,
,![]() ,
,
∵![]() ,
,![]() .∴
.∴![]() .
.
又∵![]() ,∴
,∴![]() ,
,
在![]() 和
和![]() 中
中
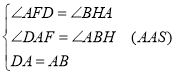
∴![]() ≌
≌![]() .∴
.∴![]() .
.
⑤正确:∵![]() ,
,![]() ,
,
∴![]() ,又∵
,又∵![]() ,∴
,∴![]()
又∵![]() ,∴
,∴![]() ,又∵
,又∵![]() ,∴
,∴![]()

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案【题目】学校组织八年级350名学生参加“汉字听写”大赛,赛后发现所有参赛学生的成绩均不低于50分,为了更好地了解本次大赛的成绩分布情况,随机抽取了其中若干名学生的成绩作为样本进行整理,得到下列不完整的统计图表:
成绩x/分 | 频数 | 频率 |
50≤x<60 | 2 | 0.04 |
60≤x<70 | 6 | 0.12 |
70≤x<80 | 9 | b |
80≤x<90 | a | 0.36 |
90≤x≤100 | 15 | 0.30 |
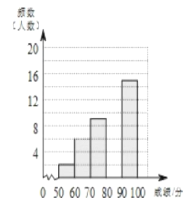
请根据所给信息,解答下列问题:
(1)求a和b的值;
(2)请补全频数分布直方图。
【题目】一种商品按销售量分三部分制定销售单价,如下表:
销售量 | 单价 |
不超过100件的部分 | 2.8元/件 |
超过100件不超过300件的部分 | 2.2元/件 |
超过300件的部分 | 2元/件 |
(1)若买100件花 元,买300件花 元;买380件花 元;
(2)小明买这种商品花了500元,求购买了这种商品多少件;
(3)若小明花了n元(n>280),恰好购买0.4n件这种商品,求n的值.