题目内容
【题目】如图所示,有一长方形的空地,长为![]() 米,宽为
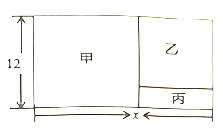
米,宽为![]() 米,建筑商把它分成甲、乙、丙三部分,甲和乙为正方形.现计划甲建筑成住宅区,乙建成商场丙开辟成公园.
米,建筑商把它分成甲、乙、丙三部分,甲和乙为正方形.现计划甲建筑成住宅区,乙建成商场丙开辟成公园.
![]() 请用含
请用含![]() 的代数式表示正方形乙的边长; ;
的代数式表示正方形乙的边长; ;
![]() 若丙地的面积为
若丙地的面积为![]() 平方米,请求出
平方米,请求出![]() 的值.
的值.
【答案】(1)(x12)米;(2)![]() 的值为20或16.
的值为20或16.
【解析】
(1)由甲和乙为正方形,且该地长为x米,宽为12米,可得出丙的长,也是乙的边长;
(2)由(1)求得丙的长,再求出丙的宽,即可得出丙的面积,由此列出方程,求解即可.
解:(1)因为甲和乙为正方形,结合图形可得丙的长为:(x12)米.
同样乙的边长也为(x12)米,
故答案为:(x12)米;
(2)结合(1)得,丙的长为:(x12)米,丙的宽为12(x12)=(24x)米,所以丙的面积为:(x12)(24x),
列方程得,(x12)(24x)=32
解方程得x1=20,x2=16.
答:![]() 的值为20或16.
的值为20或16.

练习册系列答案
相关题目