题目内容
【题目】如图,四边形ABCD中,两对角线相交于E,且E为对角线BD的中点,∠DAE=30°,∠BCE=120°.若CE=1,BC=2,则AC的长为 . 
【答案】6
【解析】解:如图,延长BC交AD的延长线于F,在AE上取一点K,使得EK=CE,连接DK、BK. 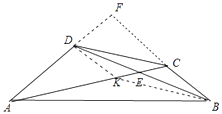
∵DE=BE,EK=CE,
∴四边形CDKB是平行四边形,
∴DK=BC=2,DK∥BF,
∵∠ACB=120°,
∴∠FCA=180°﹣120°=60°,
∵∠DAC=30°,
∴∠F=90°,
∵DK∥BF,
∴∠ADK=∠F=90°,∵∠DAK=30°,
∴AK=2DK=4,
∴AC=AK+EK+CE=4+1+1=6,
所以答案是6.
【考点精析】认真审题,首先需要了解平行四边形的判定与性质(若一直线过平行四边形两对角线的交点,则这条直线被一组对边截下的线段以对角线的交点为中点,并且这两条直线二等分此平行四边形的面积),还要掌握相似三角形的判定与性质(相似三角形的一切对应线段(对应高、对应中线、对应角平分线、外接圆半径、内切圆半径等)的比等于相似比;相似三角形周长的比等于相似比;相似三角形面积的比等于相似比的平方)的相关知识才是答题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目







