题目内容
【题目】如图，建筑物AB后有一座假山，其坡度为i=1：
，山坡上E点处有一凉亭，测得假山坡脚C与建筑物水平距离BC=25米，与凉亭距离CE=20米，某人从建筑物顶端测得E点的俯角为45°，求建筑物AB的高．（注：坡度i是指坡面的铅直高度与水平宽度的比）
【答案】解：过点E作EF⊥BC于点F，过点E作EN⊥AB于点N，
∵建筑物AB后有一座假山，其坡度为i=1：
，
∴设EF=x，则FC=x，
∵CE=20米，
∴x2+（x）2=400，
解得：x=10，
则FC=
m，
∵BC=25m，∴BF=NE=（25+）m，
∴AB=AN+BN=NE+EF=10+25+=（35+）m，
答：建筑物AB的高为（35+）m．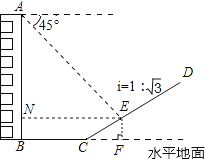
【解析】首先过点E作EF⊥BC于点F，过点E作EN⊥AB于点N，再利用坡度的定义以及勾股定理得出EF、FC的长，求出AB的长即可．
【考点精析】解答此题的关键在于理解关于坡度坡角问题的相关知识，掌握坡面的铅直高度h和水平宽度l的比叫做坡度(坡比)．用字母i表示，即i=h/l．把坡面与水平面的夹角记作A(叫做坡角)，那么i=h/l=tanA，以及对关于仰角俯角问题的理解，了解仰角：视线在水平线上方的角；俯角：视线在水平线下方的角．
【题目】中央政府为了应对因人口老龄化而造成的劳动力短缺等问题，拟定出台“延迟退休年龄政策”，为了了解人们对“延迟退休年龄政策”的态度，责成人社部进行调研，人社部从网上年龄在15～65岁的人群中随机调查100人，调查数据的频率分布直方图和支持“延迟退休”的人数与年龄的统计结果如下 
年龄 | [15，25） | [25，35） | [35，45） | [45，55） | [55，65] |
支持“延迟退休”的人数 | 15 | 5 | 15 | 28 | 17 |
（1）由以上统计数据填2×2列联表，并判断是否95%的把握认为以45岁为界点的不同人群对“延迟退休年龄政策”的支持有差异；
45岁以下 | 45岁以上 | 总计 | |
支持 | |||
不支持 | |||
总计 |
（2）若以45岁为分界点，从不支持“延迟退休”的人中按分层抽样的方法抽取8人参加某项活动，现从这8人中随机抽2人． ①抽到1人是45岁以下时，求抽到的另一人是45岁以上的概率；
②记抽到45岁以上的人数为X，求随机变量X的分布列及数学期望．
P（K2≥k0） | 0.100 | 0.050 | 0.010 | 0.001 |
k0 | 2.706 | 3.841 | 6.635 | 10.828 |
．
