题目内容
【题目】如图,等腰![]() 中,
中,![]() ,
,![]() .动点
.动点![]() 在
在![]() 上以每分钟5个单位长度的速度从
上以每分钟5个单位长度的速度从![]() 点出发向
点出发向![]() 点移动,过
点移动,过![]() 作
作![]() 交
交![]() 边于
边于![]() 点,连结
点,连结![]() 、
、![]() .设
.设![]() 点移动的时间为
点移动的时间为![]() .
.
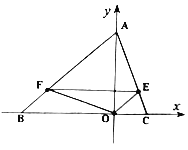
(1)求![]() 、
、![]() 两点的坐标;
两点的坐标;
(2)计算:当![]() 面积最大时,
面积最大时,![]() 的值;
的值;
(3)在(2)的条件下,边![]() 上是否还存在一个点
上是否还存在一个点![]() ,使得
,使得![]() ?若存在,请直接写出
?若存在,请直接写出![]() 点的坐标;若不存在,试说明理由.
点的坐标;若不存在,试说明理由.
【答案】(1)A(0,6),B(-8,0);(2)当t=1时,△EFO的面积达到最大值;(3)存在满足条件的D点,其坐标为(-3,0)
【解析】
(1)先根据题意得出AC两点的坐标,再设BO=x,由勾股定理求出x的值,进而可得出B点坐标;
(2)过F点作FK⊥BC于K,设F点移动的时间为t,证明△AFE∽△ABC,利用相似的性质得出EF=10-5t,从而得到S△EFO=-![]() (t-2)t,从而得出结果;
(t-2)t,从而得出结果;
(3)在(2)的条件下,E、F分别是AC、AB的中点,若使D为BC的中点时,![]() ,再由
,再由![]() 可知FO=ED,EO=FD,EF=FE,故△EFD≌△FEO,从而可得出D点坐标.
可知FO=ED,EO=FD,EF=FE,故△EFD≌△FEO,从而可得出D点坐标.
解:(1)∵CO=2,
∴C(2,0),
又∵AO=3OC=6,
∴A(0,6),
可设BO=x,且x>0,
则:BC2=(2+x)2,AB2=AO2+OB2=36+x2,
又∵BC=AB,
∴(2+x)2=36+x2,
解得:x=8,
∴B(-8,0);
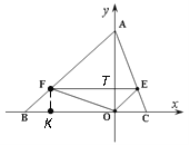
(2)过F点作FK⊥BC于K,
可设F点移动的时间为t,且0<t<2,
则:BF=5t,TO=FK=3t;
∴AT=6-3t,
又∵FE∥BC,
∴△AFE∽△ABC,
而AO⊥BC交EF于T,
则:![]() =
=![]() ,
,
∴![]() =
=![]() ,即:EF=10-5t,
,即:EF=10-5t,
故:S△EFO=![]() EF×TO=
EF×TO=![]() (10-5t)×3t,
(10-5t)×3t,
即:S△EFO=-![]() (t-2)t,
(t-2)t,
∴当t=1时,△EFO的面积达到最大值;
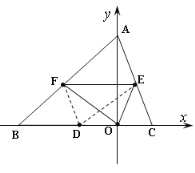
(3)在(2)的基础上,E、F分别是AC、AB的中点,
若使D为BC的中点时,
![]() ,
,
又∵![]() ,
,
∴FO=ED,EO=FD,EF=FE,
在△EFD和△FEO中,
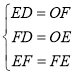 ,
,
则△EFD≌△FEO(SSS),
∵B(-8,0),C(2,0),
∴D(-3,0),
故:存在满足条件的D点,其坐标为(-3,0).