题目内容
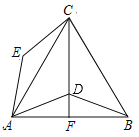
【题目】现有多个全等直角三角形,先取三个拼成如图1所示的形状,![]() 为
为![]() 的中点,
的中点,![]() 分别交
分别交![]() ,
,![]() 于
于![]() ,
,![]() ,易得
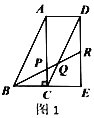
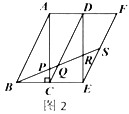
,易得![]() .若取四个直角三角形拼成如图2所示的形状,
.若取四个直角三角形拼成如图2所示的形状,![]() 为
为![]() 的中点,
的中点,![]() 分别交
分别交![]() ,
,![]() ,
,![]() 于
于![]() ,
,![]() ,
,![]() ,则
,则![]() _________.
_________.
【答案】![]()
【解析】
首先证明△BCQ∽△BES,从而可求得CQ=![]() EF,DQ=
EF,DQ=![]() EF,然后证明△BAP∽△QDR得到BP:QR=4:3从而可知:BP:PQ:QR=4:1:3,然后由DQ∥SE,可知:QR:RS=DQ:SE=3:2,从而可求得BP:PQ:QR:RS=4:1:3:2.
EF,然后证明△BAP∽△QDR得到BP:QR=4:3从而可知:BP:PQ:QR=4:1:3,然后由DQ∥SE,可知:QR:RS=DQ:SE=3:2,从而可求得BP:PQ:QR:RS=4:1:3:2.
解:(1)∵四个直角三角形是全等三角形,
∴AB=EF=CD,AB∥EF∥CD,BC=CE,AC∥DE,
∴BP:PR=BC:CE=1,
∵CD∥EF,
∴△BCQ∽△BES.
又∵BC=CE
∴CQ=![]() SE=
SE=![]() EF,
EF,
∴DQ=![]() EF,
EF,
∵AB∥CD,
∴∠ABP=∠DQR.
又∵∠BAP=∠QDR,
∴△BAP∽△QDR.
∴BP:QR=4:3.
∴BP:PQ:QR=4:1:3,
∵DQ∥SE,
∴QR:RS=DQ:SE=3:2,
∴BP:PQ:QR:RS=4:1:3:2.
故答案为:4:1:3:2

练习册系列答案
 开心练习课课练与单元检测系列答案
开心练习课课练与单元检测系列答案
相关题目