ЬтФПФкШн
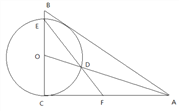
ЁОЬтФПЁПШчЭМЃЌЦНУцжБНЧзјБъЯЕжаЃЌОиаЮ OABC ЕФ ЖЅ Еу AЃЈ0ЃЌ3ЃЉЃЌCЃЈ- 1ЃЌ0ЃЉ. НЋ Ои аЮ OABC ШЦдЕуЫГЪБеыа§зЊ 900ЃЌЕУЕНОиаЮ OAЁЏBЁЏCЁЏ.НтД№ЯТСаЮЪЬтЃК
ЃЈ1ЃЉЧѓГіжБЯп BBЁЏЕФКЏЪ§НтЮіЪНЃЛ
ЃЈ2ЃЉжБЯп BBЁЏгы x жсНЛгкЕу MЁЂгы y жсНЛгкЕуNЃЌХзЮяЯп y = ax2+ bx + c ЕФЭМЯѓОЙ§ЕуCЁЂMЁЂNЃЌЧѓХзЮяЯпЕФКЏЪ§НтЮіЪН.
ЃЈ3ЃЉНЋЁїMON бижБЯп MN ЗелЃЌЕу O ТфдкЕуP ДІЃЌЧыФуХаЖЯЕу P ЪЧЗёдкХзЮяЯпЩЯЃЌЫЕУїРэгЩ.

ЁОД№АИЁПЃЈ1ЃЉy=-![]() ;(2)y=
;(2)y=![]() ;(3)ВЛдк.
;(3)ВЛдк.
ЁОНтЮіЁПЪдЬтЗжЮіЃКБОЬтПМВщЖўДЮКЏЪ§ЕФзлКЯгІгУЃЌЦфжаЩцМАЕНЕФжЊЪЖЕугаД§ЖЈЯЕЪ§ЗЈЧѓКЏЪ§НтЮіЪНКЭКЏЪ§ЭМЯѓЩЯЕуЕФвтвхЃЌОиаЮЕФаджЪгыУцЛ§ЃЌКЏЪ§КЭЗНГЬжЎМфЕФЙиЯЕЕШЃЎвЊЪьСЗеЦЮеВХФмСщЛюдЫгУЃЎ
ЃЈ1ЃЉИљОнЫФБпаЮOABCЪЧОиаЮПЩжЊBЃЈ-1ЃЌ3ЃЉЃЎИљОна§зЊЕФаджЪЃЌЕУBЁфЃЈ3ЃЌ1ЃЉЃЎ
АбBЃЈ-1ЃЌ3ЃЉЃЌBЁфЃЈ3ЃЌ1ЃЉДњШыy=mx+nжаЃЌРћгУД§ЖЈЯЕЪ§ЗЈПЩНтЕУy=-![]() ЃЎ
ЃЎ
ЃЈ2ЃЉгЩЃЈ1ЃЉЕУЃЌNЃЈ0ЃЌ![]() ЃЉЃЌMЃЈ5ЃЌ0ЃЉЃЎЩшЖўДЮКЏЪ§НтЮіЪНЮЊy=a
ЃЉЃЌMЃЈ5ЃЌ0ЃЉЃЎЩшЖўДЮКЏЪ§НтЮіЪНЮЊy=a![]() +bx+cЃЌАбCЃЈ-1ЃЌ0ЃЉЃЌMЃЈ5ЃЌ0ЃЉЃЌNЃЈ0ЃЌ
+bx+cЃЌАбCЃЈ-1ЃЌ0ЃЉЃЌMЃЈ5ЃЌ0ЃЉЃЌNЃЈ0ЃЌ![]() ЃЉДњШыЕУЃЌРћгУД§ЖЈЯЕЪ§ЗЈНтЕУЖўДЮКЏЪ§НтЮіЪНЮЊy=
ЃЉДњШыЕУЃЌРћгУД§ЖЈЯЕЪ§ЗЈНтЕУЖўДЮКЏЪ§НтЮіЪНЮЊy=![]()
![]() +2x+
+2x+![]() ЃЎ
ЃЎ
ЃЈ3ЃЉЙ§ЕуOзїODЁЭMNгкЕуDЃЌгЩMЁЂNЕуЕФзјБъЃЌПЩЧѓГіONЁЂOMЕФжЕЃЌНјЖјЧѓЕУMNЕФжЕЃЌШЛКѓПЩЧѓЕУODЕФжЕЃЌНјЖјЧѓГіOPЕФжЕЃЌЕУЕНPЕуЕФзјБъЃЌШЛКѓНЋPЕуЕФзјБъДњШыХзЮяЯпЕФНтЮіЪНЃЌМДПЩХаЖЯЕуPЪЧЗёдкХзЮяЯпЩЯЃЎ
ЪдЬтНтЮіЃКЃЈ1ЃЉгЩЬтвтЕУЃЌBЃЈ![]() ЃЌ3ЃЉЃЌ
ЃЌ3ЃЉЃЌ![]() ЃЈ3ЃЌ1ЃЉЃЌ
ЃЈ3ЃЌ1ЃЉЃЌ
ЁржБЯп![]() ЕФНтЮіЪНЮЊ
ЕФНтЮіЪНЮЊ![]() ЃЛ
ЃЛ
ЃЈ2ЃЉжБЯп![]() гы
гы![]() жсЕФНЛЕуЮЊMЃЈ5ЃЌ0ЃЉЃЌ
жсЕФНЛЕуЮЊMЃЈ5ЃЌ0ЃЉЃЌ
гы![]() жсЕФНЛЕуNЃЈ0ЃЌ
жсЕФНЛЕуNЃЈ0ЃЌ![]() ЃЉЃЌ
ЃЉЃЌ
ЩшХзЮяЯпЕФНтЮіЪНЮЊ![]() ЃЌ
ЃЌ
ЁпХзЮяЯпЙ§ЕуNЃЌ
Ёр![]() ЃЌ
ЃЌ
Ёр![]() ЃЌ
ЃЌ
ЁрХзЮяЯпЕФНтЮіЪНЮЊ![]() =
=![]() ЃЛ
ЃЛ
ЃЈ3ЃЉЙ§ЕуOзїODЁЭMNгкЕуDЃЌ
ЁпMЃЈ5ЃЌ0ЃЉЃЌNЃЈ0ЃЌ![]() ЃЉЃЌ
ЃЉЃЌ
ЁрON=![]() ЃЌOM=5ЃЌ
ЃЌOM=5ЃЌ
ЁрMN=![]() ЃЌ
ЃЌ
ЁрOD=![]() ЃЌ
ЃЌ
ЁпНЋЁїMONбижБЯпMNЗелЃЌЕуOТфдкЕуPДІЃЌ
ЁрOP=![]() ЃЌ
ЃЌ
ЁрPЃЈ2ЃЌ4ЃЉДњШыХзЮяЯпЕФНтЮіЪНЃЌ
ЕуPВЛдкХзЮяЯпЩЯЃЎ

 ЕЅдЊЦкжаЦкФЉОэЯЕСаД№АИ
ЕЅдЊЦкжаЦкФЉОэЯЕСаД№АИ