题目内容
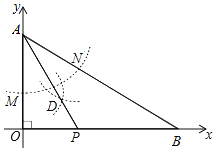
【题目】如图,已知AO为Rt△ABC的角平分线,∠ACB=90°,![]() ,以O为圆心,OC 为半径的圆分别交AO,BC于点D,E,连接ED并延长交AC于点F.
,以O为圆心,OC 为半径的圆分别交AO,BC于点D,E,连接ED并延长交AC于点F.
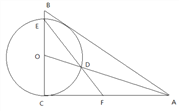
(1)求证:AB是⊙O的切线;
(2)求![]() 的值。
的值。
(3)若⊙O的半径为4,求![]() 的值.
的值.
【答案】(1)见解析;(2)![]() ;(3)
;(3)![]() .
.
【解析】分析:(1)作垂直,证半径,先根据AAS证明△OGA≌△OCA,可得OC=OG,可知OG为为⊙O的半径,可得结论;(2)设AC=4x,BC=3x,则AB=5x,根据等角的三角函数可得tan∠CAO=tan∠GAO=![]() ;(3)先根据勾股定理求得AO=
;(3)先根据勾股定理求得AO=![]() ,则求得AD=OA-OD=
,则求得AD=OA-OD=![]() .证明△DFA∽△CDA,列比例式DA:AC=AF:AD,代入可得AF的长,代入可得结论.
.证明△DFA∽△CDA,列比例式DA:AC=AF:AD,代入可得AF的长,代入可得结论.
详解:(1)证明:作OG⊥AB于点G.
∵∠ACB=∠OGA=90°,∠GAO=∠CAO,AO=AO,
∴△OGA≌△OCA,
∴OC=OG,
∵OC为⊙O的半径,
∴AB是⊙O的切线;
(2)解:设AC=4x,BC=3x,则AB=5x,
由切线长定理知,AC=AG=4x,故BG=x.
∵tan∠B=OG:BG=AC:BC=4:3,
∴OG=![]() ,
,
∴tan∠CAO=tan∠GAO=![]() =
=![]() =
=![]() ;
;
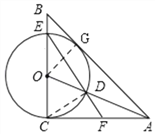
(3)解:由(2)可知 在Rt△OCA中,AO=![]()
∴AD=OA﹣OD=![]()
连接CD,则∠DCF+∠ECD=∠ECD+∠CEF,
∴∠DCF=∠CEF,
又∠CEF=∠EDO=∠FDA,
∴∠DCF=∠ADF,又∠FAD=∠DAC,
∴△DFA∽△CDA,
∴DA:AC=AF:AD,
即![]() :12=AF:
:12=AF:![]()
∴AF=![]() ,CF=12-
,CF=12-![]() =
=![]()
∴![]()

练习册系列答案
 浙江名校名师金卷系列答案
浙江名校名师金卷系列答案 全优冲刺100分系列答案
全优冲刺100分系列答案
相关题目