Question

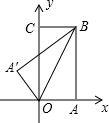
如图，把一个矩形纸片OABC放入平面直角坐标系中，使OA、OC分别落在x轴、y轴上，连接OB，将纸片OABC沿OB折叠，使点A落在A′的位置上．若OB=

5

，

BC

OC

=

1

2

，求点A′的坐标为______．

Answer 1

∵OB=

5

，

BC

OC

=

1

2

∴BC=1，OC=2
设OC与A′B交于点F，作A′E⊥OC于点E
∵纸片OABC沿OB折叠
∴OA=OA′，∠BAO=∠BA′O=90°
∵BC∥A′E
∴∠CBF=∠FA′E
∵∠AOE=∠FA′O
∴∠A′OE=∠CBF
∴△BCF≌△OA′F
∴OA′=BC=1，设A′F=x
∴OF=2-x
∴x²+1=（2-x）²，
解得x=

3

4

∴A′F=

3

4

，OF=

5

4

∵A′E=A′F×OA′÷OF=

3

5

∴OE=

4

5

∴点A’的坐标为（-

3

5

，

4

5

）．
故答案为：（-

3

5

，

4

5

）．