题目内容
已知抛物线的形状与抛物线y=-
x2相同,且对称轴为x=-
,交x轴于A、D两点(A在D左边),交y轴于B(0,-4).
(1)求抛物线的解析式;
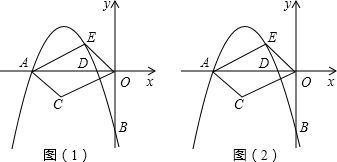
(2)如图(1),E为抛物线上在第二象限的点,连OE、AE,将线段OE沿射线EA平移,使E与A对应,O与C对应,设四边形OEAC的面积为S,问是否存在这样的点E,使S=24?若存在,请求出E点坐标,并进一步判断此时四边形OEAC的形状;若不存在,请说明理由;
(3)如图(2),在(2)的基础上,设E(xE,yE),C(xC,yC),当E点在抛物线上运动时,下列两个结论:①|xE|+|xC|的值不变;②|yE|+|yC|的值不变,有且只有一个正确,请判断正确的结论并证明求值.
| 2 |
| 3 |
| 7 |
| 2 |
(1)求抛物线的解析式;
(2)如图(1),E为抛物线上在第二象限的点,连OE、AE,将线段OE沿射线EA平移,使E与A对应,O与C对应,设四边形OEAC的面积为S,问是否存在这样的点E,使S=24?若存在,请求出E点坐标,并进一步判断此时四边形OEAC的形状;若不存在,请说明理由;
(3)如图(2),在(2)的基础上,设E(xE,yE),C(xC,yC),当E点在抛物线上运动时,下列两个结论:①|xE|+|xC|的值不变;②|yE|+|yC|的值不变,有且只有一个正确,请判断正确的结论并证明求值.

考点:二次函数综合题
专题:
分析:(1)设出函数顶点式,将B(0,-4)代入解析式即可;
(2)假设存在这样的点,根据S=24得到S?OECA=2•S△AEO=24,即S△AEO=12,然后将坐标代入求解即可.
(3)过E作 EM⊥AO于M,过C作CN⊥AO于N,将OM+ON转化为AN+ON=OA=6即可解答.
(2)假设存在这样的点,根据S=24得到S?OECA=2•S△AEO=24,即S△AEO=12,然后将坐标代入求解即可.
(3)过E作 EM⊥AO于M,过C作CN⊥AO于N,将OM+ON转化为AN+ON=OA=6即可解答.
解答:解:(1)设函数解析式为y=-
(x+
)2+c,
将B(0,-4)代入解析式得,-4=-
(0+
)2+c,
解得,c=
,
函数解析式为y=-
(x+
)2+
;
(2)依题意知OE平行且等于AC,
∴四边形OEAC为平行四边形,
又∵OA为平行四边形OEAC的对角线,
∴S?OECA=2•S△AEO=24,即S△AEO=12,
∴
•OA•|yE|=12,
又∵A(-6,0),OA=6,
yE=-
(x+
)2+
,
∴
×6×[-
(x+
)2+
]=12,
解得,x1=-3,x2=-4,
∴E1(-3,4)或E2(-4,4),
∴这样的点有两个.
当E1(-3,4)时,有AE=OE,此时平行四边形为菱形
当E2(-4,4)时,AE≠OE,AE不垂直于OE,此时四边形OEAC为平行四边形;
(3)|xE|+|xC|的值不变,|xE|+|xC|=6,
证明:过E作EM⊥AO于M,过C作CN⊥AO于N,

则|xE|=OM,|xC|=ON,
∵四边形OEAC是平行四边形,
∴OE∥AC,OE=AC,
∴△EMO≌△CNA,
∴OM=AN,
∴OM+ON=AN+ON=OA=6,即|xE|+|xC|=6.
| 2 |
| 3 |
| 7 |
| 2 |
将B(0,-4)代入解析式得,-4=-
| 2 |
| 3 |
| 7 |
| 2 |
解得,c=
| 25 |
| 6 |
函数解析式为y=-
| 2 |
| 3 |
| 7 |
| 2 |
| 25 |
| 6 |
(2)依题意知OE平行且等于AC,
∴四边形OEAC为平行四边形,
又∵OA为平行四边形OEAC的对角线,
∴S?OECA=2•S△AEO=24,即S△AEO=12,
∴
| 1 |
| 2 |
又∵A(-6,0),OA=6,
yE=-
| 2 |
| 3 |
| 7 |
| 2 |
| 25 |
| 6 |
∴
| 1 |
| 2 |
| 2 |
| 3 |
| 7 |
| 2 |
| 25 |
| 6 |
解得,x1=-3,x2=-4,
∴E1(-3,4)或E2(-4,4),
∴这样的点有两个.
当E1(-3,4)时,有AE=OE,此时平行四边形为菱形
当E2(-4,4)时,AE≠OE,AE不垂直于OE,此时四边形OEAC为平行四边形;
(3)|xE|+|xC|的值不变,|xE|+|xC|=6,
证明:过E作EM⊥AO于M,过C作CN⊥AO于N,

则|xE|=OM,|xC|=ON,
∵四边形OEAC是平行四边形,
∴OE∥AC,OE=AC,
∴△EMO≌△CNA,
∴OM=AN,
∴OM+ON=AN+ON=OA=6,即|xE|+|xC|=6.
点评:本题考查了二次函数综合题,对于存在性问题,先假设其存在,然后求解,若能的出结果,则存在,否则不存在.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
一个不透明的袋子中装有6个白球,4个黄球和5个红球,则任意摸出一个球是红球的概率是( )
A、
| ||
B、
| ||
C、
| ||
D、
|
下列计算中,不正确的是( )
| A、(-3a2b)•(-2ab2)=6a3b3 | ||||
B、(2×10n) • (
| ||||
| C、(-2×102)(-8×103)=1.6×106 | ||||
| D、(-3x)•2xy+x2y=7x2y |
 如图,OB平分∠AOC,且∠2:∠3:∠4=1:3:4,求∠1,∠2,∠3,∠4.
如图,OB平分∠AOC,且∠2:∠3:∠4=1:3:4,求∠1,∠2,∠3,∠4.