题目内容
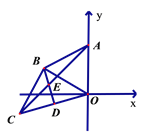
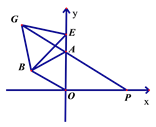
【题目】如图所示，若将类似于a、b、c、d四个图的图形称做平面图，则其顶点数、边数与区域数之间存在某种关系．观察图b和表中对应的数值，探究计数的方法并作答． 
（1）数一数每个图中各有多少个顶点、多少条边，这些边围出多少个区域并填表：
图 | a | b | c | d |
顶点数（S） | 7 | |||
边数（M） | 9 | |||
区域数（N） | 3 |
（2）根据表中数值，写出平面图的顶点数、边数、区域数之间的一种关系；
（3）如果一个平面图有20个顶点和11个区域，那么利用（2）中得出的关系可知这个平面图有条边．
【答案】
（1）解：
图 | a | b | c | d |
顶点数（S） | 4 | 7 | 8 | 10 |
边数（M） | 6 | 9 | 12 | 15 |
区域数（N） | 3 | 3 | 5 | 6 |
（2）解：观察表中数据可得；4+3﹣6=1，7+3﹣9=1，8+5﹣12=1，10+6﹣15=1
∴S+N﹣M=1；（或顶点数+区域数一边数=1）
（3）30
【解析】解： （3）由（2）得：边数=顶点数+区域数﹣1=20+11﹣1=30．
【考点精析】关于本题考查的平面图形的认识，需要了解有些几何图形的各个部分都在同一平面内，它们是平面图形才能得出正确答案．
练习册系列答案
阅读快车系列答案
相关题目
