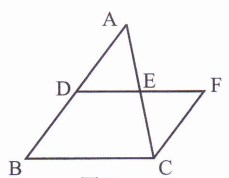
题目内容
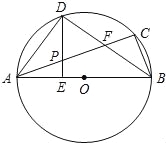
【题目】已知:如图,△ABC内接于⊙O,AB为直径,∠CBA的平分线交AC于点F,交⊙O于点D,DE⊥AB于点E,且交AC于点P,连结AD.
(1)求证:∠DAC=∠DBA;
(2)求证:P是线段AF的中点;
(3)连接CD,若CD﹦3,BD﹦4,求⊙O的半径和DE的长.
【答案】(1)证明见解析
(2)证明见解析
(3)⊙O的半径为2.5,DE的长为2.4.
【解析】
试题分析:(1)利用角平分线的性质得出∠CBD=∠DBA,进而得出∠DAC=∠DBA;
(2)利用圆周角定理得出∠ADB=90°,进而求出∠PDF=∠PFD,则PD=PF,求出PA=PF,即可得出答案;
(3)利用勾股定理得出AB的长,再利用三角形面积求出DE即可.
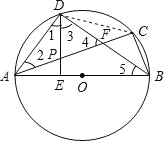
试题解析:(1)∵BD平分∠CBA,∴∠CBD=∠DBA,∵∠DAC与∠CBD都是弧CD所对的圆周角,
∴∠DAC=∠CBD,∴∠DAC=∠DBA;
(2)∵AB为直径,
∴∠ADB=90°,
∵DE⊥AB于E,
∴∠DEB=90°,
∴∠1+∠3=∠5+∠3=90°,
∴∠1=∠5=∠2,
∴PD=PA,
∵∠4+∠2=∠1+∠3=90°,且∠ADB=90°,
∴∠3=∠4,
∴PD=PF,
∴PA=PF,即P是线段AF的中点;
(3)连接CD,
∵∠CBD=∠DBA,
∴CD=AD,
∵CD﹦3,∴AD=3,
∵∠ADB=90°,
∴AB=5,
故⊙O的半径为2.5,
∵DE×AB=AD×BD,
∴5DE=3×4,
∴DE=2.4.
即DE的长为2.4.

 阅读快车系列答案
阅读快车系列答案【题目】如图所示,若将类似于a、b、c、d四个图的图形称做平面图,则其顶点数、边数与区域数之间存在某种关系.观察图b和表中对应的数值,探究计数的方法并作答. 
(1)数一数每个图中各有多少个顶点、多少条边,这些边围出多少个区域并填表:
图 | a | b | c | d |
顶点数(S) | 7 | |||
边数(M) | 9 | |||
区域数(N) | 3 |
(2)根据表中数值,写出平面图的顶点数、边数、区域数之间的一种关系;
(3)如果一个平面图有20个顶点和11个区域,那么利用(2)中得出的关系可知这个平面图有条边.
【题目】某学校积极响应上级的号召,举行了“决不让一个学生因贫困而失学”的捐资助学活动,其中6个班同学的捐款平均数如下表:
班级 | 一班 | 二班 | 三班 | 四班 | 五班 | 六班 |
捐款平均数(元) | 6 | 4.6 | 4.1 | 3.8 | 4.8 | 5.2 |
则这组数据的中位数是多少元?