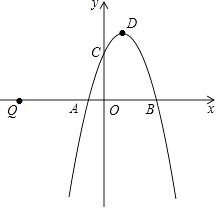题目内容
【题目】如图 1,点 A(2,1),点 A 与点 B 关于 y 轴对称,AC∥y 轴,且 AC=3,连接 BC 交 y 轴于点 D.
(1)点 B 的坐标为_____,点 C 的坐标为_____;
(2)如图 2,连接 OC,OC 平分∠ACB,求证:OB⊥OC;
(3)如图 3,在(2)的条件下,点 P 为 OC 上一点,且∠PAC=45°,求点 P 的坐标.
【答案】(1)(-2,1) (2,4);(2)见解析;(3)P(1,2)
【解析】
(1)由轴对称可得B、C点坐标;
(2)由OC 平分∠ACB,可得∠1=∠2,又∠3=∠2,可得CD=DO,CE⊥y 轴于点 E,连接 AB 交 y 轴于点 F,可证的△CDE≌△BDF(AAS),可得CD=BD,BD=CD=OD,∠DBO=∠DOB,可得OB⊥OC;
(3)连接 BP,作 PQ⊥x 轴于点 Q,由点 A,点 B 关于 y 轴对称 可得∠BAC =90,∠PAC =45,PA 平分∠CAB,可证的OB=OP,可得△BOF≌△POQ(AAS).可得PQ=BF=2,OQ=OF=1,P(1,2).
(1)B(-2,1),C(2,4).
(2)∵OC 平分∠ACB,
∴∠1=∠2,
∵AC∥y 轴,
∴∠3=∠2,
∴∠1=∠3,
∴CD=DO.
作 CE⊥y 轴于点 E,连接 AB 交 y 轴于点 F,
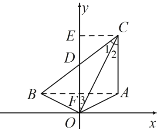
∵点 A,点 B 关于 y 轴对称,
∴BF⊥y 轴,
∴∠CED=∠BFD,
∵B(-2,1),C(2,4),
∴CE=BF=2,
在△CDE 和△BDF 中,
CED BFDCDE BDF,CE BF,
∴△CDE≌△BDF(AAS).
∴CD=BD,
∴BD=CD=OD,
∴∠DBO=∠DOB,
∵∠1+∠3+∠DBO+∠DOB=180°,
∴∠3+∠DOB=90°,
∴OB⊥OC;
(3)连接 BP,作 PQ⊥x 轴于点 Q,
∵点 A,点 B 关于 y 轴对称,
∴AB⊥y 轴,
∴∠BAC =90,
∵∠PAC =45,
∴PA 平分∠CAB,
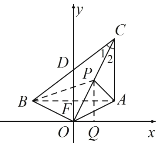
∵OC 平分∠ACB,
∴BP 平分∠ABC.
∴∠BPC=135°,
∴∠BPO=45°.
∵∠BOP=90°,
∴OB=OP,
在△BOF 和△POQ 中,
BFO PQO,BOF POQ,OB OP,
∴△BOF≌△POQ(AAS).
∴PQ=BF=2,OQ=OF=1,
∴P(1,2).