题目内容
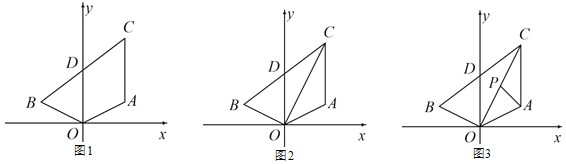
【题目】如图，二次函数y=mx2+（m2﹣m）x﹣2m+1的图象与x轴交于点A、B，与y轴交于点C，顶点D的横坐标为1．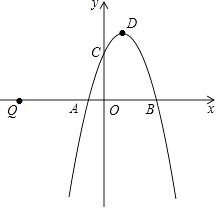
（1）求二次函数的表达式及A、B的坐标；
（2）若P（0，t）（t＜﹣1）是y轴上一点，Q（﹣5，0），将点Q绕着点P顺时针方向旋转90°得到点E．当点E恰好在该二次函数的图象上时，求t的值；
（3）在（2）的条件下，连接AD、AE．若M是该二次函数图象上一点，且∠DAE=∠MCB，求点M的坐标．
【答案】
（1）
解：∵抛物线的顶点坐标的横坐标为1，
∴ 
，
解得，m1=﹣1，m2=0（舍去）
∴二次函数的表达式为y=﹣x2+2x+3，
当y=0时，﹣x2+2x+3=0，
解得，x1=﹣1，x2=3，
∴A（﹣1，0），B（3，0），
（2）
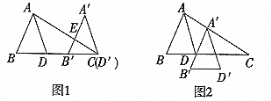
解：如图1，过点E作EH⊥y轴于点H，
∵∠PQO+∠OPQ=90°，∠OPQ+∠HPE=90°，
∴∠HPE=∠PQO，
由旋转知，PQ=PE，
在△EPH和△PQO中，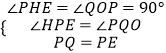 
，
∴△EPH≌△PQO，
∴EH=OP=﹣t，HP=OQ=5
∴E（﹣t，5+t）
当点E恰好在该二次函数的图象上时，有5+t=﹣t2﹣2t+3
解得t1=﹣2，t2=﹣1（由于t＜﹣1所以舍去），
（3）
解：设点M（a，﹣a2+2a+3）
①若点M在x轴上方，
如图2，过点M作MN⊥y轴于点N，
过点D作DF⊥x轴于点F．
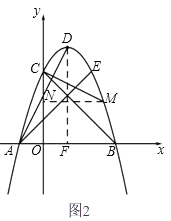
∵∠EAB=∠OCB=45°，∠DAE=∠MCB
∴∠MCN=∠DAF
∴△MCN∽△DAF，
∴ 
，即 
∴ 
，a2=0（舍去）
∴ 
，
②若点M在x轴下方，
如图3，过点M作MN⊥y轴于点N，
过点D作DF⊥x轴于点F．
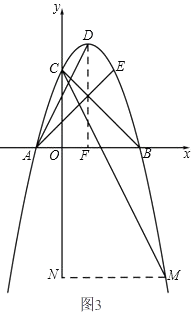
∵∠EAB=∠OCB=45°，∠DAE=∠MCB
∴∠MCN=∠ADF
∴△MCN∽△ADF
∴ 
，即 
∴a1=4，a2=0（舍去）
∴M（4，﹣5）
综上所述， 或M（4，﹣5）．
【解析】（1）利用抛物线的顶点坐标的横坐标为1建立方程即可求出M，进而得出抛物线解析式，再令y=0解一元二次方程即可得出点A，B的坐标；（2）先构造出全等三角形△EPH≌△PQO，进而得出EH=OP=﹣t，HP=OQ=5，即可得出点E的坐标，代入抛物线解析式中即可求出t；（3）分两种情况讨论计算，①点M在x轴上方时，构造相似三角形△MCN∽△DAF得出比例式建立方程即可求出点M的坐标，②点M在x轴下方时，同①的方法即可得出点M的坐标．
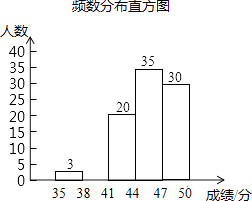
【题目】为了传承优秀传统文化，我市组织了一次初三年级1200名学生参加的“汉字听写”大赛，为了更好地了解本次大赛的成绩分布情况，随机抽取了100名学生的成绩（满分50分），整理得到如下的统计图表：
成绩（分） | 36 | 37 | 38 | 39 | 40 | 41 | 42 | 43 | 44 | 45 | 46 | 47 | 48 | 49 | 50 |
人数 | 1 | 2 | 3 | 3 | 6 | 7 | 5 | 8 | 15 | 9 | 11 | 12 | 8 | 6 | 4 |
成绩分组 | 频数 | 频率 |
35≤x＜38 | 3 | 0.03 |
38≤x＜41 | a | 0.12 |
41≤x＜44 | 20 | 0.20 |
44≤x＜47 | 35 | 0.35 |
47≤x≤50 | 30 | b |
请根据所提供的信息解答下列问题：
（1）样本的中位数是分；
（2）频率统计表中a= ， b=；
（3）请补全频数分布直方图；
（4）请根据抽样统计结果，估计该次大赛中成绩不低于41分的学生有多少人？ 
