题目内容
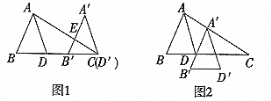
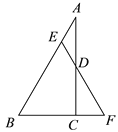
【题目】如图,在 Rt△ABC 中,∠A=30°,∠ACB=90°,点 D 为 AC 中点, 点 E 为 AB 边上一动点,AE=DE,延长 ED 交 BC 的延长线于点 F.
(1)求证:△BEF 是等边三角形;
(2)若 AB=12,求 DE 的长.
【答案】(1)见解析;(2)DE=3.
【解析】
(1)在Rt△ABC 中,∠A=30°,∠ACB=90°,可得∠B=60°,又D 为 AC 中点,AE=DE,可得∠A =∠ADE=30°,可得∠BEF= 60°,△BEF 是等边三角形.
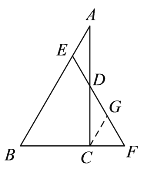
(2) 在 EF 上截取 FG=CF ,连接 CG, 可证得△ADE≌△CDG,AE=CG 设 AE=x,可得BE=12-x,CF=CG=AE=x,BF=6+x,可求x的值,可得DE的长.
(1)A =30°,∠ACB =90°,,
∴∠B=60°.
∵AE=DE,
∴∠A =∠ADE=30°,
∴∠BEF=∠A +∠ADE= 60°.
∴△BEF 是等边三角形.
(2)在 EF 上截取 FG=CF ,连接 CG,
∵∠F=60°,
∴△CFG 为等边三角形.
∴∠FGC =∠F=∠BEF=60°,
∴∠AED =∠CGD,
在△ADE 和△CDG 中,
ADE CDG,AED CGD,AD CD,
∴△ADE≌△CDG(AAS),
∴AE=CG 设 AE=x,则BE=12-x,
∵BC=6,
∴CF=CG=AE=x,
∴BF=6+x,
∴12-x=6+x,,
∴x=3,
∴DE=3.

练习册系列答案
 赢在课堂名师课时计划系列答案
赢在课堂名师课时计划系列答案
相关题目