��Ŀ����
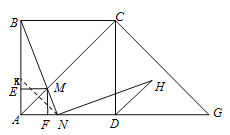
����Ŀ����14������ͼ���ڱ߳�Ϊ2��������ABCD�У�G��AD�ӳ����ϵ�һ�㣬��DG=AD������M��A��������ÿ��1����λ���ٶ�����A��C��G��·����G�������˶���M����A��G�غ��������˶�ʱ��Ϊt�롣����BM���ӳ���AG��N��

��1���Ƿ���ڵ�M��ʹ��ABMΪ���������Σ������ڣ�������M��λ�ã��������ڣ���˵�����ɣ�
��2������N��AD����ʱ����BN��HN��NH����CDG��ƽ������H����֤��BN=NH��
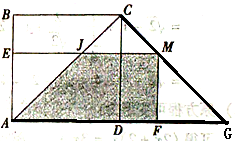
��3������M�ֱ���AB��AD�Ĵ��ߣ�����ֱ�ΪE��F������AEMF����ACG�ص����ֵ����ΪS����S�����ֵ��
���𰸡���1�������������2�������������3����t=![]() ��ʱ��S�����ֵΪ
��ʱ��S�����ֵΪ![]() .
.
��������
�����������1����ABMΪ�����������������������AM=BM����AB=BM,��AM=AB���������������ȷ��M��λ��.��2������ͬ�ǵĵ������ȿ�֤��ABN=��DNH����֤��BKN=��NDH=135��BK=DN������ASA���ж���BNK�ա�NHD����������ȫ�������εĶ�Ӧ����ȿɵ�BN=NH.��3������AEMF����ACG�ص����ַ����������������M��AC��ʱ����0<t��![]() ʱ������M��CG��ʱ����
ʱ������M��CG��ʱ����![]() <t<
<t<![]() ʱ,�ֱ���������������ʱ����AEMF����ACG�ص����ֵ����S���˶�ʱ��t֮��ĺ�����ϵʽ�����ö��κ������������������������Ե����ֵ���ٽ��бȽϣ��ҳ����ļ�Ϊ�����.
ʱ,�ֱ���������������ʱ����AEMF����ACG�ص����ֵ����S���˶�ʱ��t֮��ĺ�����ϵʽ�����ö��κ������������������������Ե����ֵ���ٽ��бȽϣ��ҳ����ļ�Ϊ�����.
���������
��1������MΪAC�е�ʱ����AM=BM,����ABMΪ���������Σ�
����M���C�غ�ʱ��AB=BM,����ABMΪ���������Σ�
����M��AC����AM=2ʱ��AM=AB,����ABMΪ����������.
֤������AB��ȡ��K,ʹAK=AN������KN.
��AB=AD,BK=AB-AK,ND=AD-AN,��BK=DN.
��DHƽ��ֱ����CDG�����CDH=45�����NDH=90+45=135.
���BKN=180-��AKN=135,���BKN=��NDH.
����Rt��ABN����ABN+��ANB=90����BN��NH,����BNH=90
���ANB+��DNH=180-��BNH=180-90=90
���ABN=��DNH.����BNK�ա�NHD��ASA��,��BN=NH.
������M��AC��ʱ����0<t��![]() ʱ����֪����AMFΪ����ֱ��������.
ʱ����֪����AMFΪ����ֱ��������.
��AM=t,��AF=FM=![]() .
.
��S=![]() .
.
����M��CG��ʱ����![]() <t<
<t<![]() ʱ,CM=t-
ʱ,CM=t-![]() ,MG=
,MG=![]() -t.
-t.
��AD=DG,��ADC=��CDG,CD=CD,
����ACD�ա�GCD��SAS��,
���ACD=��GCD=45
���ACM=��ACD+��GCD=90
���G=90-��GCD=90-45=45
���MFGΪ����ֱ��������.
��![]()

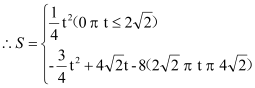
����0<t��![]() ��Χ�ڣ���t=
��Χ�ڣ���t=![]() ʱ��S�����ֵΪ
ʱ��S�����ֵΪ![]() .
.
��![]() <t<
<t<![]() ��Χ�ڣ�
��Χ�ڣ�![]() ����
����![]() ʱ��S�����ֵΪ
ʱ��S�����ֵΪ![]() .
.
��![]()
����t=![]() ��ʱ��S�����ֵΪ
��ʱ��S�����ֵΪ![]() .
.

