Question

【题目】如图，直线的解析表达式为，且与轴交于点D,直线经过点A,B,直线，交于点C．

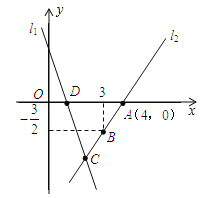
（1）求直线的解析式；

（2）求△ADC的面积；

（3）在直线上存在异于点C的另一点P，使得△ADP与△ADC的面积相等，请直接写出点P的坐标．

Answer 1

【答案】（1）直线l2的解析表达式为y＝x﹣6；（2）S△ADC＝；（3）点P的坐标为（6，3）．

【解析】

（1）由点A、B的坐标利用待定系数法即可求出直线l2的解析表达式；

（2）根据一次函数图象上点的坐标特征找出点D的坐标，联立直线AB、CD的表达式求出交点C的坐标，再根据三角形的面积公式即可求出△ADC的面积；

（3）由同底等高的三角形面积相等即可找出点P的纵坐标，再根据一次函数图象上点的坐标特征即可得出点P的坐标．

（1）设直线l2的解析表达式为y=kx+b（k≠0），

把A（4，0）、B（3，）代入表达式y=kx+b，

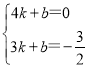，解得：，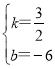

∴直线l2的解析表达式为y=x-6．

（2）当y=-3x+3=0时，x=1，

∴D（1，0）．

联立y=-3x+3和y=x-6，

解得：x=2，y=-3，

∴C（2，-3），

∴S△ADC=×3×|-3|=．

（3）∵△ADP与△ADC底边都是AD，△ADP与△ADC的面积相等，

∴两三角形高相等．

∵C（2，-3），

∴点P的纵坐标为3．

当y=x-6=3时，x=6，

∴点P的坐标为（6，3）．