题目内容
如图,△ABC中,∠C=90°,BC=3,AC=4,D为AC上一点,以CD为直径的⊙O切AB于点E.求⊙O的半径长.
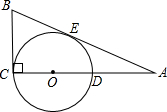

连接OE,
∵∠C=90°,CD是⊙O的直径,
∴BC是⊙O的切线,
∵BE是⊙O的切线,
∴BE=BC=3,
在Rt△ABC中,
∴AB=
=
=5,
∴AE=AB-BE=5-3=2,
∵AB是⊙O切线,切点为E,
∴∠AEO=90°,
∴tanA=
,
∵在△ABC中,tanA=
∴
=
∴OE=
×AE=
×2=
,即为⊙O的半径长.

∵∠C=90°,CD是⊙O的直径,
∴BC是⊙O的切线,
∵BE是⊙O的切线,
∴BE=BC=3,
在Rt△ABC中,
∴AB=
| BC2+AC2 |
| 32+42 |
∴AE=AB-BE=5-3=2,
∵AB是⊙O切线,切点为E,
∴∠AEO=90°,
∴tanA=
| OE |
| AE |
∵在△ABC中,tanA=
| BC |
| AC |
∴
| OE |
| AE |
| BC |
| AC |
∴OE=
| BC |
| AC |
| 3 |
| 4 |
| 3 |
| 2 |


练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目


 O与⊙O交于点D,与PA的延长线交于点E.
O与⊙O交于点D,与PA的延长线交于点E.

