Question

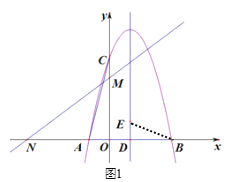
【题目】如图1，抛物线y1=x2tx-t+2与x轴交于点A，B(点A在点B的左侧)，过y轴上的点C(0，4)，直线y2=kx+3交x轴，y轴于点M、N，且ON=OC.

(1)求出t与k的值.

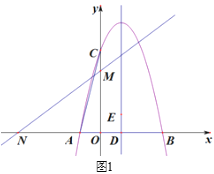
(2)抛物线的对称轴交x轴于点D，在x轴上方的对称轴上找一点E，使△BDE与△AOC相似，求出DE的长.

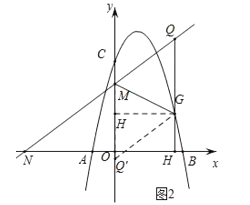
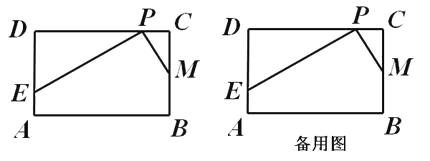
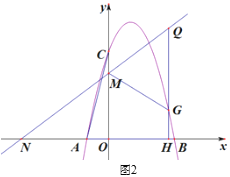
(3)如图2，过抛物线上动点G作GH⊥x轴于点H，交直线y2=kx+3于点Q，若点Q′是点Q关于直线MG的对称点，是否存在点G(不与点C重合)，使点Q′落在y轴上？，若存在，请直接写出点G的横坐标；若不存在，请说明理由.

Answer 1

【答案】(1)t=-2，k=；(2)或8；(3)；；；.

【解析】

（1）将C(0，4) 代入抛物线y1=x2tx-t+2，求出t的值，由ON=OC可写出点N坐标，将其代入直线y2=kx+3即可求出k；

（2）因为∠AOC=∠EDB=90°已经确定，所以分两种情况讨论，当△AOC∽△BDE和△AOC∽△EDB时，通过对应边成比例可分别求出DE的长；

（3）先根据题意画出图形，通过轴对称的性质证明四边形QMQ'G为菱形，分别用字母表示出Q、G的坐标，分两种情况讨论求出GQ'的长度，利用三角函数可求出点G的横坐标.

解：（1）将点C(0，4)代入抛物线y1=x2tx-t+2，得-t+2=4，∴t=-2，

∴抛物线y1=x2x+4，

∵ON=OC，∴N（-4，0），

将N（-4，0）代入直线y2=kx+3，得-4k+3=0，∴，

∴直线y2=x+3，

∴t=-2，.

（2）如图1，链接BE，在y1=x2x+4中，当y=0时，解得：，，

∴A（-1，0），B（3，0），对称轴为x=，

∴D（1，0），

∴AO=1，CO=4，BD=2，∠AOC=∠EDB=90°，

①当△AOC∽△BDE时，

，即，

∴DE=8，

②当△AOC∽△EDB时，

，即，

∴DE=，

综上：DE=或8；

（3）如图2，点Q'是点Q关于直线MG的对称点，且点Q'在y轴上，

由轴对称的性质知：QM= Q'M，QG= Q'G，∠Q'MG= ∠QMG，

∵QG⊥x轴，∴QG∥y轴，

∴∠Q'MG=∠QGM，

∴∠QMG=∠QGM，

∴QM=QG，

∴QM=Q'M=QG=Q'G，

∴四边形QMQ'G为菱形，

设G（a，a2a+4），则Q（a，a+3），

过点G作GH⊥y轴于点H，

∵GQ'∥QN，

∴∠GQ'H=∠NMO，

在Rt△NMO中，

NM=，

∴，

∴，

①当点G在直线MN下方时，QG= Q'G=，

∴，解得：，；

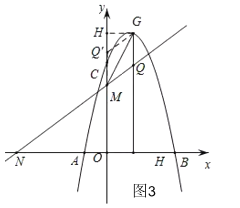
②如图3，当点G在直线MN上方时，QG= Q'G=，

∴，解得：，.

综上所述：点G的横坐标为，，或.