题目内容
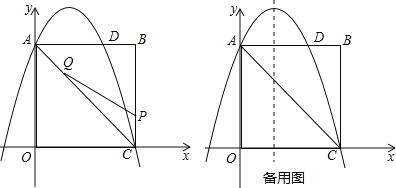
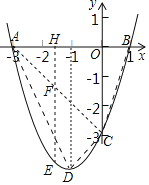
【题目】在平面直角坐标系xOy中(如图),已知经过点A(﹣3,0)的抛物线y=ax2+2ax﹣3与y轴交于点C,点B与点A关于该抛物线的对称轴对称,D为该抛物线的顶点.
(1)直接写出该抛物线的对称轴以及点B的坐标、点C的坐标、点D的坐标;
(2)联结AD、DC、CB,求四边形ABCD的面积;
(3)联结AC.如果点E在该抛物线上,过点E作x轴的垂线,垂足为H,线段EH交线段AC于点F.当EF=2FH时,求点E的坐标.
【答案】(1)对称轴为x=﹣1,点B、C、D的坐标依次为(1,0),(0,﹣3),(﹣1,﹣4);(2)9;(3)(﹣2,﹣3).
【解析】
(1)由题意可知该抛物线的对称轴为直线x=![]() =﹣1,而点A(-3,0),求出点B的坐标,进而求解;
=﹣1,而点A(-3,0),求出点B的坐标,进而求解;
(2)根据题意将四边形ABCD的面积分解为△DAM、梯形DMOC、△BOC的面积和,即可求解;
(3)根据题意设点E(x,x2+2x-3),则点F(x,-x-1),求出EF、FH长度的表达式,即可求解.
解:(1)∵该抛物线的对称轴为直线x=![]() =﹣1,而点A(﹣3,0),
=﹣1,而点A(﹣3,0),
∴点B的坐标为(1,0),
∵c=﹣3,故点C的坐标为(0,﹣3),
∵函数的对称轴为x=﹣1,故点D的坐标为(﹣1,﹣4);
(2)过点D作DM⊥AB,垂足为M,
则OM=1,DM=4,AM=2,OB=1,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴ ![]() ;
;
(3)设直线AC的表达式为:y=kx+b,则![]() ,解得:
,解得:![]() ,
,
故直线AC的表达式为:y=﹣x﹣3,
将点A的坐标代入抛物线表达式得:9a﹣6a﹣3=0,解得:a=1,
故抛物线的表达式为:y=x2+2x﹣3,
设点E(x,x2+2x﹣3),则点F(x,﹣x﹣1),
则EF=(﹣x﹣1)﹣(x2+2x﹣3)=﹣x2﹣3x,FH=x+3,
∵EF=2FH,
∴﹣x2﹣3x=2(x+3),解得:x=﹣2或﹣3(舍去﹣3),
故m=﹣2.
故点E的坐标为:(﹣2,﹣3).