题目内容
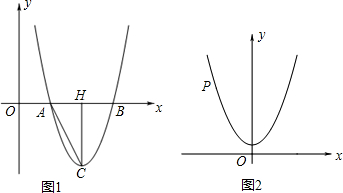
如图1,抛物线y=a(x-2)2-2的顶点为C,抛物线与x轴交于A,B两点(其中A点在B点的左边),CH⊥AB于H,且tan∠ACH=
(1)求抛物线的解析式;
(2)在坐标平面内是否存在一点D,使得以O、B、C、D为顶点的四边形是等腰梯形?若存在,求所有的符合条件的D点的坐标;若不存在,请说明理由;
(3)如图2,将(1)中的抛物线平移,使其顶点在y轴的正半轴上,在y轴上是否存在一点M,使得平移后的抛物线上的任意一点P到x轴的距离与P点到M的距离相等?若存在,求出M点的坐标;若不存在,请说明理由.
| 1 |
| 2 |
(1)求抛物线的解析式;
(2)在坐标平面内是否存在一点D,使得以O、B、C、D为顶点的四边形是等腰梯形?若存在,求所有的符合条件的D点的坐标;若不存在,请说明理由;
(3)如图2,将(1)中的抛物线平移,使其顶点在y轴的正半轴上,在y轴上是否存在一点M,使得平移后的抛物线上的任意一点P到x轴的距离与P点到M的距离相等?若存在,求出M点的坐标;若不存在,请说明理由.

(1)由抛物线的解析式知:C(2,-2);
在Rt△ACH中,CH=2,AH=CH•tan∠ACH=2×
=1,则 A(1,0)、B(3,0).
将点A的坐标代入抛物线的解析式中,得:
0=a(1-2)2-2,则 a=2;
∴抛物线的解析式:y=2(x-2)2-2=2x2-8x+6.
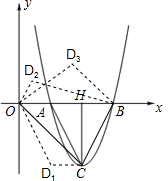 (2)假设存在符合条件的D点.
(2)假设存在符合条件的D点.
连接OC、BC,由B(3,0)、C(2,-2)得:
OB=3;∠HOC=∠HCO=45°,OC=2
;tan∠HBC=2,BC=
.
①当OB∥CD1、OD1=BC时,如右图;
点D1的横坐标的纵坐标与BH长相同,则点D1(1,-2).
②当OD2∥BC、OC=BD2时;
tan∠D2OB=tan∠HBC=2,则 直线OD2:y=2x;
设点D2(x,2x),则:BD2=
=
,
由OC=BD2得:2
=
,解得:x=
,x=1(舍)
即点D2(
,
).
③当OC∥BD3、OD3=BC时;
∠D3BO=∠HOC=45°,即tan∠D3BO=1,可设 B(x,3-x);
由OD3=BC=
,得:
x2+(3-x)2=5,解得 x=2,x=1(舍)
即点D3(2,1).
综上可知,存在符合条件的点D,且坐标为:(1,-2)、(
,
)、(2,1).
(3)设平移后的抛物线解析式为:y=2x2+m,那么其顶点为(0,m),若存在符合条件的点M,则M(0,2m);(m>0)
设P(x,2x2+m),则:
PM2=(x-0)2+(2x2+m-2m)2=x2+4x4-4mx2+m2,P到x轴的距离:2x2+m;
依题意有:x2+4x4-4mx2+m2=(2x2+m)2,解得:m=
.
∴存在符合条件的点M,且坐标为 M(0,
).
在Rt△ACH中,CH=2,AH=CH•tan∠ACH=2×
| 1 |
| 2 |
将点A的坐标代入抛物线的解析式中,得:
0=a(1-2)2-2,则 a=2;
∴抛物线的解析式:y=2(x-2)2-2=2x2-8x+6.
 (2)假设存在符合条件的D点.
(2)假设存在符合条件的D点.连接OC、BC,由B(3,0)、C(2,-2)得:
OB=3;∠HOC=∠HCO=45°,OC=2
| 2 |
| 5 |
①当OB∥CD1、OD1=BC时,如右图;
点D1的横坐标的纵坐标与BH长相同,则点D1(1,-2).
②当OD2∥BC、OC=BD2时;
tan∠D2OB=tan∠HBC=2,则 直线OD2:y=2x;
设点D2(x,2x),则:BD2=
| (x-3)2+(2x-0)2 |
| 5x2-6x+9 |
由OC=BD2得:2
| 2 |
| 5x2-6x+9 |
| 1 |
| 5 |
即点D2(
| 1 |
| 5 |
| 2 |
| 5 |
③当OC∥BD3、OD3=BC时;
∠D3BO=∠HOC=45°,即tan∠D3BO=1,可设 B(x,3-x);
由OD3=BC=
| 5 |
x2+(3-x)2=5,解得 x=2,x=1(舍)
即点D3(2,1).
综上可知,存在符合条件的点D,且坐标为:(1,-2)、(
| 1 |
| 5 |
| 2 |
| 5 |
(3)设平移后的抛物线解析式为:y=2x2+m,那么其顶点为(0,m),若存在符合条件的点M,则M(0,2m);(m>0)
设P(x,2x2+m),则:
PM2=(x-0)2+(2x2+m-2m)2=x2+4x4-4mx2+m2,P到x轴的距离:2x2+m;
依题意有:x2+4x4-4mx2+m2=(2x2+m)2,解得:m=
| 1 |
| 8 |
∴存在符合条件的点M,且坐标为 M(0,
| 1 |
| 4 |

练习册系列答案
相关题目


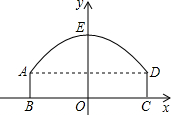 线段BC的中垂线为y轴,建立平面直角坐标系,y轴是抛物线的对称轴,顶点E到坐标原点O的距离为6m.
线段BC的中垂线为y轴,建立平面直角坐标系,y轴是抛物线的对称轴,顶点E到坐标原点O的距离为6m.
 ,0),∠ABO=60度.
,0),∠ABO=60度.
