题目内容
【题目】如图,正方形ABCD的边长为3cm,动点P从B点出发以3cm/s的速度沿着边BC﹣CD﹣DA运动,到达A点停止运动;另一动点Q同时从B点出发,以1cm/s的速度沿着边BA向A点运动,到达A点停止运动.设P点运动时间为x(s),△BPQ的面积为y(cm2),则y关于x的函数图象是( )
A.
B.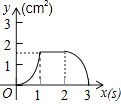
C.
D.
【答案】C
【解析】解:由题意可得BQ=x.
①0≤x≤1时,P点在BC边上,BP=3x,
则△BPQ的面积= ![]() BPBQ,
BPBQ,
解y= ![]() 3xx=
3xx= ![]() x2;故A选项错误;
x2;故A选项错误;
②1<x≤2时,P点在CD边上,
则△BPQ的面积= ![]() BQBC,
BQBC,
解y= ![]() x3=
x3= ![]() x;故B选项错误;
x;故B选项错误;
③2<x≤3时,P点在AD边上,AP=9﹣3x,
则△BPQ的面积= ![]() APBQ,
APBQ,
解y= ![]() (9﹣3x)x=
(9﹣3x)x= ![]() x﹣
x﹣ ![]() x2;故D选项错误.
x2;故D选项错误.
故答案为:C.
此题是一道分段函数的应用题,根据自变量的取值范围分三段:①0≤x≤1时,P点在BC边上;y是关于x的二次函数。①0≤x≤1时,P点在BC边上,y是关于x的一次函数③2<x≤3时,P点在AD边上,y是关于x的二次函数。分别求出函数关系式,即可求得正确的选项。

练习册系列答案
 应用题天天练四川大学出版社系列答案
应用题天天练四川大学出版社系列答案
相关题目