题目内容
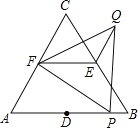
【题目】如图,△ABC和△FPQ均是等边三角形,点D、E、F分别是△ABC三边的中点,点P在AB边上,连接EF、QE.若AB=6,PB=1,则QE= .
【答案】2.
【解析】
试题分析:连结FD,根据等边三角形的性质,由△ABC为等边三角形得到AC=AB=6,∠A=60°,再根据点D、E、F分别是等边△ABC三边的中点,则AD=BD=AF=3,DP=2,EF为△ABC的中位线,于是可判断△ADF为等边三角形,得到∠FDA=60°,利用三角形中位线的性质得EF∥AB,EF=![]() AB=3,根据平行线性质得∠1+∠3=60°;又由于△PQF为等边三角形,则∠2+∠3=60°,FP=FQ,所以∠1=∠2,然后根据“SAS”判断△FDP≌△FEQ,所以DP=QE=2.
AB=3,根据平行线性质得∠1+∠3=60°;又由于△PQF为等边三角形,则∠2+∠3=60°,FP=FQ,所以∠1=∠2,然后根据“SAS”判断△FDP≌△FEQ,所以DP=QE=2.
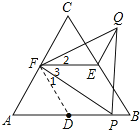
解:连结FD,如,
∵△ABC为等边三角形,
∴AC=AB=6,∠A=60°,
∵点D、E、F分别是等边△ABC三边的中点,AB=6,PB=1,
∴AD=BD=AF=3,DP=DB﹣PB=3﹣1=2,EF为△ABC的中位线,
∴EF∥AB,EF=![]() AB=3,△ADF为等边三角形,
AB=3,△ADF为等边三角形,
∴∠FDA=60°,
∴∠1+∠3=60°,
∵△PQF为等边三角形,
∴∠2+∠3=60°,FP=FQ,
∴∠1=∠2,
∵在△FDP和△FEQ中
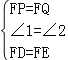 ,
,
∴△FDP≌△FEQ(SAS),
∴DP=QE,
∵DP=2,
∴QE=2.
故答案为:2.

练习册系列答案
相关题目