Question

【题目】已知:△ABC为等边三角形

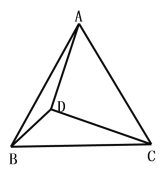
（1）若D为△ABC外一点，满足∠CDB=30,求证：

（2）若D为△ABC内一点，DC=3,DB=4,DA=5,求∠CDB的度数

（3）若D为△ABC内一点，DA=4,DB=,DC=则AB= (直接写出答案)

Answer 1

【答案】（1）详见解析；（2）150；（3）

【解析】

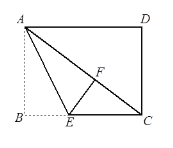
(1)以BD为边作等边△BDQ，易证△ABD≌△CBQ得AD=CQ再证∠CDQ=90得.

(2) 把△ACD绕点C顺时针旋转60°得到△BCQ，如图，连接DQ，根据旋转的性质得∠DCQ=60°，CD=CQ=3，QB=AD=5，则可判断△CDQ为等边三角形，所以DQ=4，∠BDE=60°，再利用勾股定理的逆定理证明△BDQ为直角三角形，∠QDB=90°，从而得到∠CDB=150°．

(3)同②可得∠ADB=150°，解构造30°直角三角形即可求出AB.

(1)证明：以BD为边作等边△BDQ，连接QC，

∵:△ABC、△BDQ都是等边三角形，

∴∠ABC=∠DBQ=∠BDQ=60°，BA=BC，BD=BQ,

∴∠ABD=∠CBQ，

在△ABD和△CBQ中

，

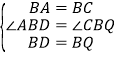∴△ABD≌△CBQ(SAS)，

∴AD=CQ

又∵∠CDB=30，

∴∠CDQ=90

∴

∴

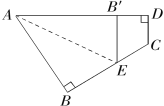
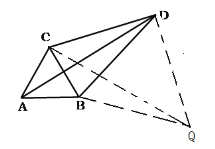
（2）解： 把△ACD绕点C逆时针旋转60°得到△BCQ，如图，连接DQ，

∵△ABC为等边三角形，

∴BA=BC，∠ABC=60°，

∴∠QCD=60°，CD=CQ=3，QB=AD=5，

∴△CDQ为等边三角形，

∴DE=4，∠DQC=60°，

在△BDQ中，∵DQ=3，BD=4，BQ=5，

∴DQ2+BD2=BQ2，

∴△DEC为直角三角形，∠QDC=90°，

∴∠CDB=60°+90°=150°．

(3)AB=

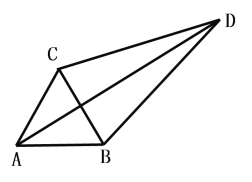
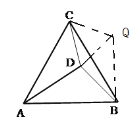
解：把△ACD绕点A逆时针旋转60°得到△BCQ，如图，连接DQ，

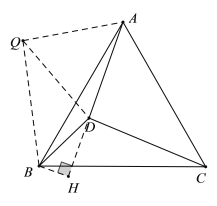
同可得②BQ= DC=，AD=AQ=DQ=4，DB=，

∴DQ2+BD2=BQ2，∠ADB=150°，

过B点作BH垂直AD，交AD延长线于H，

∴∠BDH=30°，

∴BH=BD=，DH=3，

∴AH=AD+DH=3+4=7，

∴AB===

故答案为：