题目内容

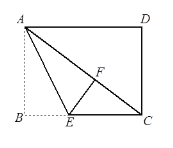
【题目】如图，已知在长方形ABCD中，将△ABE沿着AE折叠至△AEF的位置，点F在对角线AC上，若BE=3，EC=5，则线段CD的长是__________.

【答案】6

【解析】

由折叠可得：∠AFE=∠B=90°，依据勾股定理可得：Rt△CEF中，CF4．设AB= x，则AF=x ，AC=x+4，再根据勾股定理，可得Rt△ABC中，AB2+BC2=AC2，即x2+82=（x+4）2，解方程即可得出AB的长，由矩形的性质即可得出结论．

由折叠可得：AB=AF，BE=FE=3，∠AFE=∠B=90°，∴Rt△CEF中，CF4．

设AB= x，则AF=x ，AC=x+4．

∵Rt△ABC中，AB2+BC2=AC2，∴x2+82=（x+4）2，解得：x=6，∴AB=6．

∵ABCD是矩形，∴CD=AB=6．

故答案为：6．

练习册系列答案
相关题目

【题目】如图，在平面鱼角坐标系xOy中，A（﹣3，0），点B为y轴正半轴上一点，将线段AB绕点B旋转90°至BC处，过点C作CD垂直x轴于点D，若四边形ABCD的面积为36，则线AC的解析式为_____．

【题目】对任意一个三位数n，如果n满足各数位上的数字互不相同，且都不为零，那么称这个数为“相异数” ．将一个“相异数”任意两个数位上的数字对调后可以得到三个不同的新三位数，把这三个新三位数的和与111的商记为F(n)．例如n=123，对调百位与十位上的数字得到213，对调百位与个位上的数字得到321，对调十位与个位上的数字得到132，这三个新三位数的和为213+321+132=666，666÷111=6，所以F(123) =6．

（1）计算：F(315)，F(746)；

（2）若s、t都是“相异数”，其中s=100x+42，t=160+y（1≤x≤9，1≤y≤9，x、y都是正整数），当F(s)+F(t)=17时，求x、y的值.

【题目】在平面直角坐标系中，第1个正方形ABCD的位置如图所示，点A的坐标为（1，0），点D的坐标为（0，2）．延长CB交x轴于点A1，作第2个正方形A1B1C1C；延长C1B1交x轴于点A2，作第3个正方形A2B2C2C1…按这样的规律进行下去，第2个正方形的面积为_____；第2011个正方形的面积为_____．

【题目】如图，已知△ABC中，AB＝BC，D为AC中点，过点D作DE∥BC，交AB于点E．

（1）求证：AE＝DE；

（2）若∠C＝65°，求∠BDE的度数．

【题目】如图，已知抛物线ｙ＝ｘ－ａｘ＋ａ－4ａ－4与ｘ轴相交于点A和点B，与ｙ轴相交于点D（0，8），直线DC平行于ｘ轴，交抛物线于另一点C，动点P以每秒2个单位长度的速度从C点出发，沿C→D运动，同时，点Q以每秒1个单位长度的速度从点A出发，沿A→B运动，连接PQ、CB，设点P运动的时间为t秒．

（１）求ａ的值；（２）当四边形ODPQ为矩形时，求这个矩形的面积；（３）当四边形PQBC的面积等于14时，求t的值．（４）当t为何值时，△PBQ是等腰三角形？（直接写出答案）

【题目】已知:△ABC为等边三角形

（1）若D为△ABC外一点，满足∠CDB=30,求证：

（2）若D为△ABC内一点，DC=3,DB=4,DA=5,求∠CDB的度数

（3）若D为△ABC内一点，DA=4,DB=,DC=则AB= (直接写出答案)

【题目】如图，抛物线y＝－x 2＋bx＋c与x轴交于A、B两点，与y轴交于点C，已知经过B、C两点的直线的表达式为y＝－x＋3．

(1)求抛物线的函数表达式；

(2)点P(m，0)是线段OB上的一个动点，过点P作y轴的平行线，交直线BC于D，交抛物线于E，EF∥x轴，交直线BC于F，DG∥x轴，FG∥y轴，DG与FG交于点G．设四边形DEFG的面积为S，当m为何值时S最大，最大值是多少？

(3)在坐标平面内是否存在点Q，将△OAC绕点Q逆时针旋转90°，使得旋转后的三角形恰好有两个顶点落在抛物线上．若存在，求出所有符合条件的点Q的坐标；若不存在，请说明理由．

【题目】下列调查中，调查方式选择最合理的是　　

A. 为了解安徽省中学生的课外阅读情况，选择全面调查

B. 调查七年级某班学生打网络游戏的情况，选择抽样调查

C. 为确保长征六号遥二火箭成功发射，应对零部件进行全面调查

D. 为了解一批袋装食品是否含有防腐剂，选择全面调查

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网