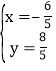Question

【题目】已知抛物线，其中是常数，该抛物线的对称轴为直线．

（）求该抛物线的函数解析式．

（）把该抛物线沿轴向上平移多少个单位后，得到的抛物线与轴只有一个公共点．

Answer 1

【答案】（1）；（2）

【解析】试题分析：

（1）把抛物线的解析式整理为一般形式，由此可得到其对称轴的表达式，结合对称轴是直线即可解出“m”的值，从而可求得其解析式；

（2）设把该抛物线向上平移个单位长度后与轴只有一个公共点，由此可得新的解析式的表达式，再由“△=”即可求得的值.

试题解析：

（1）∵可化为： ，

∴该抛物线的对称轴为直线： ，

又∵该抛物线的对称轴为：直线，

∴，解得： ，

∴抛物线的解析式为： ；

（）设原抛物线向上平移个单位后与轴只有1个公共点，则平移后抛物线解析式为：

，

∵它与轴只有一个公共点，

∴，解得： ，

即，将该抛物线向上平移个单位长度后，新抛物线与轴只有1个公共点.