题目内容
 如图,已知点C是AB上一点,△ACM、△CBN都是等边三角形.说明AN=MB.
如图,已知点C是AB上一点,△ACM、△CBN都是等边三角形.说明AN=MB.分析:根据等边三角形性质得出AC=CM,CN=CB,∠ACM=∠BCN=60°,求出∠ACN=∠BCM,根据SAS证出△ACN≌△MCB即可.
解答:证明:∵△ACM、△CBN都是等边三角形,
∴AC=CM,CN=CB,∠ACM=∠BCN=60°,
∴∠ACM+∠MCN=∠BCN+∠MCN,
∴∠ACN=∠BCM,
∵在△ACN和△MCB中
,
∴△ACN≌△MCB(SAS),
∴AN=MB.
∴AC=CM,CN=CB,∠ACM=∠BCN=60°,
∴∠ACM+∠MCN=∠BCN+∠MCN,
∴∠ACN=∠BCM,
∵在△ACN和△MCB中
|
∴△ACN≌△MCB(SAS),
∴AN=MB.
点评:本题考查等边三角形的性质和全等三角形的性质和判定,关键是推出△ACN≌△MCB.

练习册系列答案
 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案
相关题目
 如图,已知点D是AB边的中点,AF∥BC,CG:GA=3:1,BC=8,则AF=
如图,已知点D是AB边的中点,AF∥BC,CG:GA=3:1,BC=8,则AF=
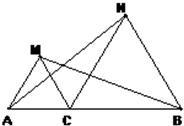 20、如图,已知点C是AB上一点,△ACM、△CBN都是等边三角形.
20、如图,已知点C是AB上一点,△ACM、△CBN都是等边三角形. 如图,已知点C是
如图,已知点C是