题目内容
 如图,已知点C是
如图,已知点C是 |
| AB |
30
30
度; CD=8-4
| 3 |
8-4
厘米.| 3 |
分析:易证得△AOB是等边三角形,则∠AOB=∠OAB=60°,AB=OA=8厘米;由圆心角、弧、弦的关系可知∠AOD=
∠AOB=30°,所以通过解直角△AOD求得OD=4
厘米,故CD=OC-OD=OA-OD=8-4
(厘米).
| 1 |
| 2 |
| 3 |
| 3 |
解答:解:如图,∵OA=OB,∠OAB=60°,
∴△AOB是等边三角形,则∠AOB=∠OAB=60°,AB=OA=8厘米.
又∵C是
的中点,
∴∠AOD=
∠AOB=30°,AB⊥OC,
∴OD=OAcos30°=4
(厘米)
∴CD=OC-OD=OA-OD=8-4
(厘米).
故答案是:8-4
.
∴△AOB是等边三角形,则∠AOB=∠OAB=60°,AB=OA=8厘米.
又∵C是
 |
| AB |
∴∠AOD=
| 1 |
| 2 |
∴OD=OAcos30°=4
| 3 |
∴CD=OC-OD=OA-OD=8-4
| 3 |
故答案是:8-4
| 3 |
点评:本题考查了垂径定理、勾股定理.此类在圆中涉及弦长、半径、圆心角的计算的问题,常把半弦长,半圆心角,圆心到弦距离转换到同一直角三角形中,然后通过直角三角形予以求解.

练习册系列答案
相关题目
 如图,已知点D是AB边的中点,AF∥BC,CG:GA=3:1,BC=8,则AF=
如图,已知点D是AB边的中点,AF∥BC,CG:GA=3:1,BC=8,则AF=
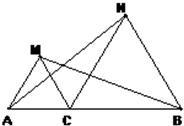 20、如图,已知点C是AB上一点,△ACM、△CBN都是等边三角形.
20、如图,已知点C是AB上一点,△ACM、△CBN都是等边三角形. 如图,已知点C是AB上一点,△ACM、△CBN都是等边三角形.说明AN=MB.
如图,已知点C是AB上一点,△ACM、△CBN都是等边三角形.说明AN=MB.