题目内容
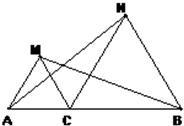 20、如图,已知点C是AB上一点,△ACM、△CBN都是等边三角形.
20、如图,已知点C是AB上一点,△ACM、△CBN都是等边三角形.(1)说明AN=MB;
(2)将△ACM绕点C按逆时针旋转180°,使A点落在CB上,请对照原题图画出符合要求的图形;
(3)在(2)所得到的图形中,结论“AN=BM”是否成立?若成立,请说明理由;若不成立,也请说明理由.
分析:(1)根据题意求得△MCB≌△ACN即可.
(2)本题考查的是考生的画图能力以及空间想象能力.
(3)与(1)题相同,证明△ACN≌△BCM即可.
(2)本题考查的是考生的画图能力以及空间想象能力.
(3)与(1)题相同,证明△ACN≌△BCM即可.
解答:解:(1)已知三角形ANC以及三角形CNB为等边三角形,
故AC=CM,CN=CB,∠NCA=∠MCB,
故△MCB≌△ACN.(SAS)
故AN=MB.
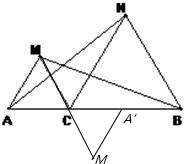 (2)如右图.
(2)如右图.
(3)如图:已知△CBN与△ACM是等边三角形,
故BC=NC,CM=AC,∠NCB=∠MCA=60°.
则∠MCB=∠ACN,
故△CBM≌△CNA,
可推出AN=BM.
故AC=CM,CN=CB,∠NCA=∠MCB,
故△MCB≌△ACN.(SAS)
故AN=MB.
 (2)如右图.
(2)如右图.(3)如图:已知△CBN与△ACM是等边三角形,
故BC=NC,CM=AC,∠NCB=∠MCA=60°.
则∠MCB=∠ACN,
故△CBM≌△CNA,
可推出AN=BM.
点评:本题综合考查全等三角形,等边三角形和四边形的有关知识,注意三角形全等的综合应用.

练习册系列答案
 科学实验活动册系列答案
科学实验活动册系列答案
相关题目
 如图,已知点D是AB边的中点,AF∥BC,CG:GA=3:1,BC=8,则AF=
如图,已知点D是AB边的中点,AF∥BC,CG:GA=3:1,BC=8,则AF=
 如图,已知点C是
如图,已知点C是
 如图,已知点C是AB上一点,△ACM、△CBN都是等边三角形.说明AN=MB.
如图,已知点C是AB上一点,△ACM、△CBN都是等边三角形.说明AN=MB.