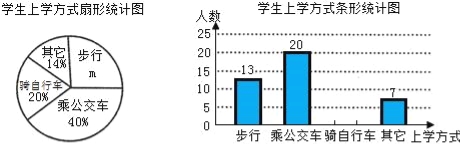
题目内容
【题目】如图,PQ∥MN,A、B分别为直线MN、PQ上两点,且∠BAN=45°,若射线AM绕点A顺时针旋转至AN后立即回转,射线BQ绕点B逆时针旋转至BP后立即回转,两射线分别绕点A、点B不停地旋转,若射线AM转动的速度是a°/秒,射线BQ转动的速度是b°/秒,且a、b满足|a﹣5|+(b﹣1)2=0.(友情提醒:钟表指针走动的方向为顺时针方向)
(1)a= ,b= ;
(2)若射线AM、射线BQ同时旋转,问至少旋转多少秒时,射线AM、射线BQ互相垂直.
(3)若射线AM绕点A顺时针先转动18秒,射线BQ才开始绕点B逆时针旋转,在射线BQ到达BA之前,问射线AM再转动多少秒时,射线AM、射线BQ互相平行?

【答案】(1)a=5,b=1;(2)t=15(s);(3)15,22.5.
【解析】
(1)依据|a﹣5|+(b﹣1)2=0,即可得到a,b的值;
(2)依据∠ABO+∠BAO=90°,∠ABQ+∠BAM=180°,即可得到射线AM、射线BQ第一次互相垂直的时间;
(3)分两种情况讨论,依据∠ABQ'=∠BAM“时,BQ'∥AM“,列出方程即可得到射线AM、射线BQ互相平行时的时间.
解:(1)|a﹣5|+(b﹣1)2=0,
∴a﹣5=0,b﹣1=0,
∴a=5,b=1,
故答案为:5,1;
(2)设至少旋转t秒时,射线AM、射线BQ互相垂直.
如图,设旋转后的射线AM、射线BQ交于点O,则BO⊥AO,
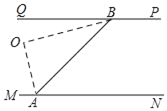
∴∠ABO+∠BAO=90°,
∵PQ∥MN,
∴∠ABQ+∠BAM=180°,
∴∠OBQ+∠OAM=90°,
又∵∠OBQ=t°,∠OAM=5t°,
∴t°+5t°=90°,
∴t=15(s);
(3)设射线AM再转动t秒时,射线AM、射线BQ互相平行.
如图,射线AM绕点A顺时针先转动18秒后,AM转动至AM'的位置,∠MAM'=18×5=90°,
分两种情况:
①当9<t<18时,∠QBQ'=t°,∠M'AM“=5t°,
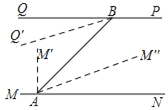
∵∠BAN=45°=∠ABQ,
∴∠ABQ'=45°﹣t°,∠BAM“=5t﹣45°,
当∠ABQ'=∠BAM“时,BQ'∥AM“,
此时,45°﹣t°=5t﹣45°,
解得t=15;
②当18<t<27时,∠QBQ'=t°,∠NAM“=5t°﹣90°,
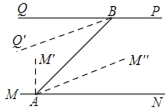
∵∠BAN=45°=∠ABQ,
∴∠ABQ'=45°﹣t°,∠BAM“=45°﹣(5t°﹣90°)=135°﹣5t°,
当∠ABQ'=∠BAM“时,BQ'∥AM“,
此时,45°﹣t°=135°﹣5t,
解得t=22.5;