题目内容
【题目】结合数轴与绝对值的知识回答下列问题:

(1)数轴上表示4和1的两点之间的距离是________;表示![]() 和2两点之间的距离是______;一般地,数轴上表示数
和2两点之间的距离是______;一般地,数轴上表示数![]() 和数
和数![]() 的两点之间的距离等于
的两点之间的距离等于![]() .如果表示数
.如果表示数![]() 和
和![]() 的两点之间的距离是3,那么
的两点之间的距离是3,那么![]() _______.
_______.
(2)若数轴上表示数![]() 的点位于
的点位于![]() 与2之间,求
与2之间,求![]() 的值;
的值;
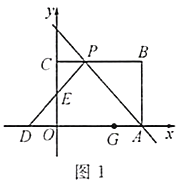
(3)受(2)的启发,当数![]() 的点在图1什么位置时,
的点在图1什么位置时,![]() 的值最小,最小值是多少?
的值最小,最小值是多少?
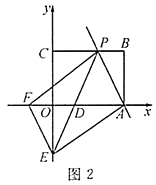
(4)有理数![]() 、
、![]() 、
、![]() 在数轴上对应的位置如图2所示,试化简:
在数轴上对应的位置如图2所示,试化简:![]() .
.
【答案】(1) 3 , 5 ,![]() 或1;(2)6;(3)7;(4)3a-c
或1;(2)6;(3)7;(4)3a-c
【解析】
(1)根据两点间的距离公式即可求解;
(2)先计算绝对值,再合并同类项即可求解;
(3)受(2)的启发,可知当数a的点位于5与2之间位置时,|a+5|+|a2|的值最小,进一步得到最小值;
(4)利用绝对值的意义化简,再合并同类项即可求解.
(1)数轴上表示4和1的两点之间的距离是41=3;表示3和2两点之间的距离是2(3)=5;
依题意有|a(2)|=3,
解得a=5或1.
故填:3 , 5 ,![]() 或1;
或1;
(2)∵数a的点位于4与2之间,
∴|a+4|+|a2|
=a+4a+2
=6;
(3)当数a的点在图1的5与2之间位置时,|a+5|+|a2|的值最小,最小值是2(5)=7;
(4)依题意有ba<0,bc<0,a+b>0,ab>0,
则|ba||bc|+|a+b|+|ab|=b+a+bc+a+b+ab=3ac.

【题目】某工厂一周计划每日生产自行车100辆,由于工人实行轮休,每日上班人数不一定相等,实际每日生产量与计划量相比情况如下表(以计划量为标准,增加的车辆数记为正数,减少的车辆数记为负数):
星期 | 一 | 二 | 三 | 四 | 五 | 六 | 日 |
增减(辆) | -1 | +3 | -2 | -4 | +7 | -5 | -10 |
(1)生产量最多的一天比生产量最少的一天多生产多少辆?
(2)本周总的生产量是多少辆?