题目内容
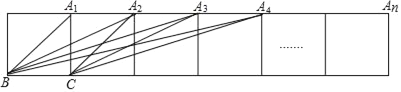
【题目】如图，把n个边长为1的正方形拼接成一排，求得tan∠BA1C=1，tan∠BA2C=
，tan∠BA3C=
，计算tan∠BA4C=_____，…按此规律，写出tan∠BAnC=_____（用含n的代数式表示）．
【答案】
； 
．
【解析】
试题过点C作CH⊥BA4于H，根据正方形的性质、勾股定理分别先求出A4C和A4B，再根据三角形的面积公式求出CH，根据勾股定理得出A4H，根据正切的概念求出tan∠BA4C，最后总结规律解答．
解：如图，过点C作CH⊥BA4于H，
由勾股定理得BA4＝
＝
，A4C＝
＝
，∵S△BA4C＝
×BC×1＝，
∴×BA4×CH＝××CH =，解得CH＝
，则A4H＝
＝
，
∴tan∠BA4C＝
＝.
∵tan∠BA1C＝1，tan∠BA2C＝
，tan∠BA3C＝
，tan∠BA4C＝.
且1＝12－1＋1，3＝22－2＋1，7＝32－3＋1，13＝42－4＋1，
∴tan∠BAnC＝
.
故答案为
，.
练习册系列答案
相关题目
【题目】某自行车厂一周计划生产1400辆自行车，平均每天生产200辆，由于各种原因实际每天生产量与计划量相比有出入．下表是某周的生产情况（超产为正、减产为负）：
星期 | 一 | 二 | 三 | 四 | 五 | 六 | 日 |
增减 |
|
|
|
|
|
|
|
（1）根据记录可知前三天共生产______辆．
（2）产量最多的一天比产量最少的一天多生产_______辆．
（3）该厂实行每周计件工资制，每生产一辆车可得60元，若超额完成任务，则超过部分每辆另奖15元；少生产一辆扣15元，那么该厂工人这一周的工资总额是多少？
