题目内容
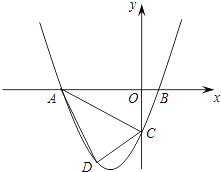
【题目】某市为解决农村燃气困难,在P处建立了一个燃气站,从P站分别向A、B、C村铺设燃气管道。已知B村在A村的北偏东60°方向,距离A村2.4km,C村在A村的正东方向,距离A村1.8km,要使此工程费用最省,管道PA+PB+PC之和需最短,则最短长度为______________km.

【答案】3
【解析】
先证明△ABC内总存在一点P与三个顶点的连线的夹角相等,此时该点到三个顶点的距离之和最小.然后根据这个原理找到点P,把△APC绕点A逆时针旋转60°得△ADE,证得△ABE是直角三角形,用勾股定理求出BE,即可得出PA+PB+PC之和的最短值。
解:先证明结论:△ABC内总存在一点P与三个顶点的连线的夹角相等,此时该点到三个顶点的距离之和最小.
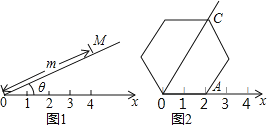
如图1, P为△ABC内一点,∠APB=∠BPC=120°,
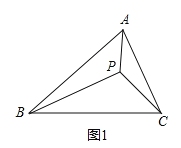
证明:如图2,将△ACP绕点A逆时针旋转60°得到△ADE,

∴∠PAD=60°,△PAC≌△DAE,
∴PA=DA、PC=DE、∠APC=∠ADE=120°,
∴△APD为等边三角形,
∴PA=PD,∠APD=∠ADP=60°,
∴∠APB+∠APD=120°+60°=180°,∠ADP+∠ADE=180°,即B、P、D、E四点共线,
∴PA+PB+PC=PD+PB+DE=BE.
∴PA+PB+PC的值最小.
解决问题:
如图3,将三个村连接为△ABC,由上可知,当∠APB=∠APC=∠BPC=120°时,AP+BP+PC的值最小.
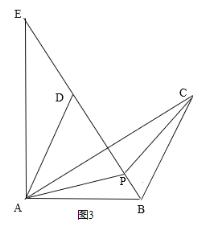
把△APC绕点A逆时针旋转60°得△ADE,
∴∠PAD=60°,AE=AC=2.4 km
由上可知B、P、D、E共线,且AP+BP+PC=BE,∠PAB=∠DAE,
∵B村在A村的北偏东60°方向, C村在A村的正东方向,
∴∠BAC=30°,
∴∠PAB+∠PAC=∠DAE+∠PAB=30°,
∴∠BAE=∠DAE+∠PAB+∠PAD=90°,
在Rt△ABE中,
![]()
∴PA+PB+PC=3km
故答案为:3

 名校课堂系列答案
名校课堂系列答案