题目内容
【题目】阅读材料,回答以下问题:
我们知道,二元一次方程有无数个解,在平面直角坐标系中,我们标出以这个方程的解为坐标的点,就会发现这些点在同一条直线上.
例如![]() 是方程
是方程![]() 的一个解,对应点
的一个解,对应点![]() ,如下图所示,我们在平面直角坐标系中将其标出,另外方程的解还有对应点
,如下图所示,我们在平面直角坐标系中将其标出,另外方程的解还有对应点![]() 将这些点连起来正是一条直线,反过来,在这条直线上任取一点,这个点的坐标也是方程
将这些点连起来正是一条直线,反过来,在这条直线上任取一点,这个点的坐标也是方程![]() 的解.所以,我们就把条直线就叫做方程
的解.所以,我们就把条直线就叫做方程![]() 的图象.
的图象.
一般的,任意二元一次方程解的对应点连成的直线就叫这个方程的图象.请问:
(1)已知![]() 、
、![]() 、
、![]() ,则点__________(填“A或
,则点__________(填“A或![]() 或
或![]() ”)在方程
”)在方程![]() 的图象上.
的图象上.
(2)求方程![]() 和方程
和方程![]() 图象的交点坐标.
图象的交点坐标.
(3)已知以关于![]() 的方程组
的方程组![]() 的解为坐标的点在方程
的解为坐标的点在方程![]() 的图象上,当
的图象上,当![]() 时,化简
时,化简![]() .
.

【答案】(1)C;(2)(3,1);(3)![]()
【解析】
(1)利用图象法即可解决问题;
(2)求出方程组的解,即为两个方程的图象的交点坐标;
(3)解方程组求出m的值,根据绝对值的性质进行化简即可.
解:(1)如图,观察图象可知:点C在方程2xy=1的图象上,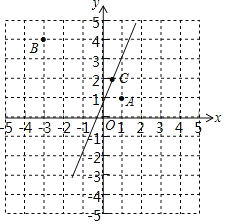
故答案为C.
(2)由![]() ,
,
解得![]() ,
,
∴方程2x+3y=9和方程3x4y=5图象的交点坐标为(3,1);
(3)由![]() ,解得
,解得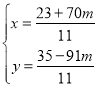 ,
,
∵x+y=5,
∴![]() +
+ ![]() =5,
=5,
∴m=![]() ,
,
当t>![]() 时,
时,![]() |17t|=t+2+17t=36t.
|17t|=t+2+17t=36t.

练习册系列答案
相关题目
【题目】某工厂计划生产![]() 两种产品共10件,其生产成本和销售价如下表所示:
两种产品共10件,其生产成本和销售价如下表所示:
产品 |
|
|
成本(万元/件) | 3 | 5 |
售价(万元/件) | 4 | 7 |
(1)若工厂计划获利14万元,则应分别生产![]() 两种产品多少件?
两种产品多少件?
(2)若工厂投入资金不多于44万元,且获利不少于14万元,则工厂有哪些生产方案?
(3)在第(2)的条件下,哪种方案获利最大;最大利润是多少?