题目内容
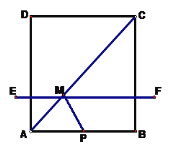
【题目】如图，正方形ABCD的边长AB是方程
的一个根，动点P从A至B以3cm/s的速度移动，动直线EF从与AB重合的位置开始向上以1cm/s速度移动（EF∥AB），EF交AD、AC、BC于E、M、F。设运动时间为t秒.
（1）当t=1时，四边形MFBP的面积为 .用t表示△APM的面积为 .
（2）在某一时刻t，使△APM与四边形MFBP的面积相等，求t的值.
【答案】（1）19，
；（2）6．
【解析】
（1）先解一元二次方程得出正方形的边长，然后分别用t表示出AP，AE，EM，MF，FB，PB．根据梯形的面积公式和三角形的面积公式计算即可；
（2）根据“△APM与四边形MFBP的面积相等”列方程，求解即可．
（1）（x-21）（x+1）=0，解得：x=21或x=－1（舍去），∴正方形的边长为21．AP=3t，AE=BF=t．
∵ABCD是正方形，∴∠DAC=45°，∴△MEA是等腰直角三角形，∴EM=EA=t，∴MF=21-t，PB=21-3t，∴四边形MFBP的面积=
（MF+PB）BF=（21-t+21-3t）t=
，当t=1时，四边形MFBP的面积=21-2=19．
△APM的面积=APAE=3tt=．
故答案为：19，．
（2）由（1）可得：
，解得：t=0（舍去），t=6．
答：t的值为6．
练习册系列答案
相关题目
