Question

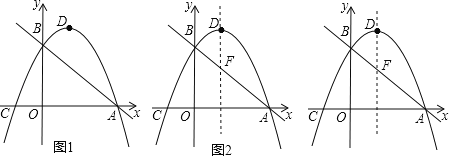
【题目】如图1，在平面直角坐标系中，直线y=﹣x+与x轴交于点A，与y轴交于点B；抛物线y=ax2+bx+（a≠0）过A，B两点，与x轴交于另一点C（﹣1，0），抛物线的顶点为D．

（1）求出A，B两点的坐标；

（2）求抛物线的解析式及顶点D的坐标；

（3）在直线AB上方的抛物线上有一动点E，求出点E到直线AB的距离的最大值；

（4）如图2，直线AB与抛物线的对称轴相交于点F，点P在坐标轴上，且点P到直线BD，DF的距离相等，请直接写出点P的坐标．

Answer 1

【答案】（1）点AB的坐标分别为（3，0）、（0，）；（2）y＝﹣x2+x+，D的坐标为（1，3）；（3）当x＝时，EF有最大值为；（4）点P的坐标为（0，1）或（﹣，0）或（0，）或（7，0）．

【解析】

（1）令x=0，则y，令y=0，则x=3，即可求解；

（2）将点A、C的坐标代入二次函数表达式得：，解得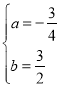：，即可求解；

（3）E到直线AB的距离=EF=EHsin∠FHE=EHcos∠BAC，即可求解；

（4）分当点P在∠BDF平分线上、外角平分线上两种情况，分别求解即可．

（1）令x=0，则y，令y=0，则x=3，即点A的坐标为（3，0）、B的坐标（0，）；

（2）将点A、C的坐标代入二次函数表达式得：，解得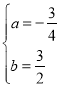：，抛物线的表达式为：yx2x，定点D的坐标为（1，3）；

（3）过点E作EH∥y轴交AB于点H，过点E作EF⊥AB．设E（x，），则H（x，），∴EH==．

∵A的坐标为（3，0）、B的坐标（0，），∴OA=3，OB=，∴AB=，∴cos∠BAC=．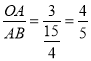

E到直线AB的距离=EF=EHsin∠FHE=EHcos∠BAC=（）x2x=，当x时，EF有最大值为；

（4）①当点P在∠BDF平分线上时，则角平分线与y轴的交点P1、x轴的交点P2为所求．

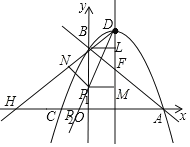
过点P1作⊥DM交于点M，作P1N⊥BD交于点N，则：P1M=P1N=1，将点B、D坐标代入一次函数表达式并解得：函数表达式为：yx，则点H坐标（﹣3，0），∴HB=．

∵sin∠P1BN=sin∠HOB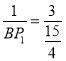，，∴，∴BP1∴OP1==1，∴故点P1（0，1），则直线DP1的表达式为：y=2x+1，令y=0，则x，即点P2（，0）；

②当点P在当点P在∠BDF的外交平分线上时，此时点P所在的直线与直线P1P2所在的直线垂直，设直线PD的解析式为y=，把D（1，3）代入得：b=，∴y=，令x=0，得y=，令y=0，得x=7，∴点P的坐标为（0，）或（7，0）；

综上所述：点P的坐标为（0，1）或（，0）或（0，）或（7，0）．