��Ŀ����
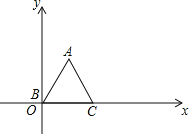
����Ŀ����ͼ����֪������y��ax2+bx+5��x�ύ��A����1��0����B��5��0�����㣨��A�ڵ�B����ࣩ����y�ύ�ڵ�C��
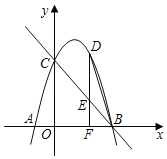
��1���������ߵĽ���ʽ��
��2����D�ǵ�һ�������������ϵ�һ�����㣨���C��B���غϣ�������D��DF��x���ڵ�F����ֱ��BC�ڵ�E������BD��ֱ��BC�ܷ�ѡ�BDF�ֳ����֮��Ϊ2��3�������֣����ܣ��������D�����ꣻ�����ܣ���˵�����ɣ�
��3����MΪ�����߶Գ�����һ���㣬ʹ�á�MBCΪֱ�������Σ���ֱ��д����M�����꣮
���𰸡���1��y����x2+4x+5����2������D������Ϊ��![]() ��
��![]() ����
����![]() ��
��![]() ��ʱ��ֱ��BC�ѡ�BDF�ֳ����֮��Ϊ2��3�������֣���3������������M�������Ϊ��2��7������2����3������2��6������2����1����
��ʱ��ֱ��BC�ѡ�BDF�ֳ����֮��Ϊ2��3�������֣���3������������M�������Ϊ��2��7������2����3������2��6������2����1����
��������
��1������������x���������������������ʽ���г���Ԫһ�η�����![]() ����˷����鼴����������ߵĽ���ʽ��
����˷����鼴����������ߵĽ���ʽ��
��2�����ͼ���֪��BDE�͡�BEF�ǵȸߵ������ɴ˵ó����ǵ�����ȼ�ΪDE��EF��2��3��������������������������ľ��빫ʽ���ɵó����̣��ⷽ�����D�����ꣻ
��3�������������MBCΪֱ��������ʱM�����꼴��.
��1����A����1��0����B��5��0������y��ax2+bx+5��
�ã�![]() ��
��
���![]() ��
��
�������߽���ʽΪy����x2+4x+5��
��2���ܣ�
��ֱ��BC�Ľ���ʽΪy��kx+b��
��C��0��5����B��5��0�������![]()
![]() ��
��
���![]() ��
��
����ֱ��BC�Ľ���ʽΪy����x+5��
��D��x����x2+4x+5������E��x����x+5����F��x��0������0��x��5����
��DE����x2+4x+5������x+5������x2+5x��EF����x+5��
��DE��EF��2��3ʱ��S��BDE��S��BEF��2��3��
������x2+5x��������x+5����2��3��
������3x2��17x+10��0��
���x1��![]() ��x2��5����ȥ������ʱD������Ϊ��
��x2��5����ȥ������ʱD������Ϊ��![]() ��
��![]() ����
����
��DE��EF��3��2ʱ��S��BDE��S��BEF��3��2��������x2+5x��������x+5����3��2��
������2x2��13x+15��0��
���x/span>1��![]() ��x2��5����ȥ������ʱD������Ϊ��
��x2��5����ȥ������ʱD������Ϊ��![]() ��
��![]() ����
����
��������������D��������![]() ��
��![]() ����
����![]() ��
��![]() ��ʱ��ֱ��BC�ѡ�BDF�ֳ����֮��Ϊ2��3�������֣�
��ʱ��ֱ��BC�ѡ�BDF�ֳ����֮��Ϊ2��3�������֣�
��3�������ߵĶԳ���Ϊֱ��x��2����ͼ��
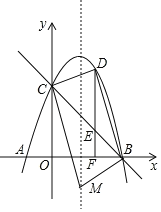
��M��2��t����
��B��5��0����C��0��5����
��BC2��52+52��50��MC2��22+��t��5��2��t2��10t+29��MB2����2��5��2+t2��t2+9��
��BC2+MC2��MB2ʱ����BCMΪֱ�������Σ���BCM��90������50+t2��10t+29��t2+9�����t��7����ʱM�������Ϊ��2��7����
��BC2+MB2��MC2ʱ����BCMΪֱ�������Σ���CBM��90������50+t2+9��t2��10t+29�����t����3����ʱM�������Ϊ��2����3����
��MC2+MB2��BC2ʱ����BCMΪֱ�������Σ���CMB��90������t2��10t+29+t2+9��50�����t1��6��t2����1����ʱM�������Ϊ��2��6����2����1����
��������������������M���������2��7������2����3������2��6������2����1����