题目内容
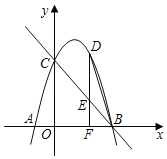
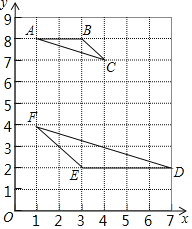
【题目】如图,双曲线y=![]() (x>0)经过△OAB的顶点A和OB的中点C,AB∥x轴,点A的坐标为(2,3),BE⊥x轴,垂足为E.
(x>0)经过△OAB的顶点A和OB的中点C,AB∥x轴,点A的坐标为(2,3),BE⊥x轴,垂足为E.

(1)确定k的值: ;
(2)计算△OAB的面积;
(3)若点D(3,b)在双曲线y=![]() (x>0)上,直线AD的解析式为y=mx+n,请直接写出不等式mx+n<
(x>0)上,直线AD的解析式为y=mx+n,请直接写出不等式mx+n<![]() 的解集: .
的解集: .
【答案】(1)6;(2)9;(3)0<x<2或x>3
【解析】
(1)将点代入求值即可.
(2) 过点C作CF⊥x轴,垂足为F,可得 △OCF∽△OBE,将点坐标代入求出AB的长,利用面积公式即可算出.
(3)将点D代入求出b的值,再根据不等式解出即可.
(1)将点A(2,3)代入y=![]() (x>0)得:k=6,
(x>0)得:k=6,
故答案为6;
(2)过点C作CF⊥x轴,垂足为F,

∴CF∥BE,
∴△OCF∽△OBE,
∵C为OB的中点,即![]() =
=![]() ,
,
∴CF=![]() BE=
BE=![]() ,
,
∵C在双曲线y=![]() 上,
上,
∴C(4,![]() ),
),
∴OF=4,OE=8,
∴AB=8﹣2=6,
得:S△AOB=![]() ×6×3=9;
×6×3=9;
(3)将D(3,b)代入反比例解析式y=![]() ,
,
得:b=![]() =2,
=2,
∴点D坐标为(3,2),
∴不等式mx+n<![]() 的解集是0<x<2或x>3,
的解集是0<x<2或x>3,
故答案为0<x<2或x>3.

练习册系列答案
相关题目