题目内容
【题目】在平面直角坐标系![]() 中,抛物线
中,抛物线![]() 的顶点为
的顶点为![]() ,直线
,直线![]() 与抛物线交于点
与抛物线交于点![]() (点
(点![]() 在点
在点![]() 的左侧).
的左侧).

(1)求点![]() 坐标;
坐标;
(2)横、纵坐标都是整数的点叫做整点.记线段![]() 及抛物线在
及抛物线在![]() 两点之间的部分围成的封闭区域(不含边界)记为
两点之间的部分围成的封闭区域(不含边界)记为![]() .
.
①当![]() 时,结合函数图象,直接写出区域
时,结合函数图象,直接写出区域![]() 内的整点个数;
内的整点个数;
②如果区域![]() 内有2个整点,请求出
内有2个整点,请求出![]() 的取值范围.
的取值范围.
【答案】(1)A(a,0);(2)①4;②![]()
【解析】
(1)根据抛物线顶点坐标求法求解即可;
(2)①画出图像,根据图像以及整点的概念求解即可;
②由①推出a<0,分别求出有2个整点和3个整点时a的取值,再得出取值范围.
解:(1)∵抛物线的解析式为:![]() ,
,
∴可得顶点坐标为:A(a,0);
(2)①∵a=0,
∴抛物线表达式为:![]() ,
,
令![]() ,
,
解得:x1=![]() ,x2=
,x2=![]() ,
,
∵![]() ,
,![]() ,
,
∴区域![]() 内的整点有(0,1),(0,2),(1,2),(1,3)共4个整点;
内的整点有(0,1),(0,2),(1,2),(1,3)共4个整点;
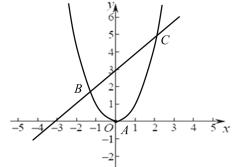
②由①可知当a=0时有4个整点,
当a>0时,对称轴在y轴右侧,此时有更多整点,
∴a<0,
∵抛物线的解析式为:![]() ,
,
∴抛物线的顶点在x轴,开口向上,
当抛物线在直线y=x+3左侧且两者相切时,没有整点,
当抛物线向右平移时,第一个整点为(-1,1),代入抛物线,
![]() ,
,
解得:a=-2或0(舍),
第二个整点为(0,2),代入抛物线,
![]() ,
,
解得:a=![]() (舍)或
(舍)或![]() ,
,
第三个整点为(0,1),代入抛物线,
![]() ,
,
解得:a=1(舍)或-1,
综上:a的取值范围是:![]() .
.

【题目】2020年3月“停课不停学”期间,某校采用简单随机抽样的方式调查本校学生参加第一天线上学习的时长,将收集到的数据制成不完整的频数分布表和扇形图,如下所示:
组别 | 学习时长(分钟) | 频数(人) |
第1组 | x≤40 | 3 |
第2组 | 40<x≤60 | 6 |
第3组 | 60<x≤80 | m |
第4组 | 80<x≤100 | 18 |
第5组 | 100<x≤120 | 14 |

(1)求m,n的值;
(2)学校有学生2400人,学校决定安排老师给““线上学习时长”在x≤60分钟范围内的学生打电话了解情况,请你根据样本估计学校学生“线上学习时长”在x≤60分钟范围内的学生人数.