题目内容

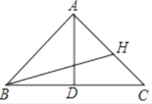
【题目】如图，把Rt△ABC绕点A逆时针旋转44°，得到Rt△AB′C′，点C′恰好落在边AB上，连接BB′，则∠BB′C′=__________________．

【答案】22°

【解析】

根据旋转的性质可以得到对应的角相等和对应的边相等，所以得出△ABB′是等腰三角形，利用等腰三角形的性质和三角形的内角和即可得出结果．

解：∵Rt△ABC绕点A逆时针旋转44°得到Rt△AB′C′，

∴∠BAC=∠BAB′=44°，∠ABC=∠AB′C′=46°，AB=AB′，

∴△ABB′是等腰三角形，

∴∠AB′B=∠ABB′，

∵∠B′AB+∠AB′B+∠ABB′=180°，

∴∠AB′B=(180°-44°)÷2=68°，

∴∠C′B′B=68°-46°=22°．

故答案为：22°．

练习册系列答案
相关题目

【题目】如图，在△ABC中，已知AB=AC=5，BC=6，且△ABC≌△DEF，将△DEF与△ABC重合在一起，△ABC不动，△DEF运动，并满足：点E在边BC上沿B到C的方向运动，且DE始终经过点A，EF与AC交于M点．

（1）求证：△ABE∽△ECM；

（2）探究：在△DEF运动过程中，重叠部分能否构成等腰三角形？若能，求出BE的长；若不能，请说明理由；

（3）当线段BE为何值时，线段AM最短，最短是多少？

【题目】函数y1=x（x≥0），y2=（x＞0）的图象如图所示，则结论：①两函数图象的交点A的坐标为（3，3）；②当x＜3时，y2＞y1；③当x=1时，BC=8；④当x逐渐增大时，y1随着x的增大而增大，y2随着x的增大而减小．其中正确结论的序号是（　　）

A. ①③④ B. ①②③④ C. ②③④ D. ①③

【题目】小明和爸爸从家步行去公园，爸爸先出发一直匀速前行，小明后出发．家到公园的距离为2500 m，如图是小明和爸爸所走的路程s(m)与步行时间t(min)的函数图象．

(1)直接写出小明所走路程s与时间t的函数关系式；

(2)小明出发多少时间与爸爸第三次相遇？

(3)在速度都不变的情况下，小明希望比爸爸早20 min到达公园，则小明在步行过程中停留的时间需作怎样的调整？

【题目】（7分）某兴趣小组开展课外活动．如图，A，B两地相距12米，小明从点A出发沿AB方向匀速前进，2秒后到达点D，此时他（CD）在某一灯光下的影长为AD，继续按原速行走2秒到达点F，此时他在同一灯光下的影子仍落在其身后，并测得这个影长为1.2米，然后他将速度提高到原来的1.5倍，再行走2秒到达点H，此时他（GH）在同一灯光下的影长为BH（点C，E，G在一条直线上）．

（1）请在图中画出光源O点的位置，并画出他位于点F时在这个灯光下的影长FM（不写画法）；

（2）求小明原来的速度．

【题目】如图，在△ABC中，AB＝10，BC＝12，BC边上的中线AD＝8．

（1）证明：△ABC为等腰三角形；

（2）点H在线段AC上，试求AH＋BH＋CH的最小值．

【题目】我市大力发展绿色交通，构建公共绿色交通体系，“共享单车”的投入使用给人们的出行带来便利．小明随机调查了若干市民租用共享单车的骑车时间t（单位：分），将获得的数据分成四组，绘制了如图统计图，请根据图中信息，解答下列问题：

（1）这次被调查的总人数是______；

（2）补全条形统计图；

（3）在扇形统计图中，求表示A组（t≤10分）的扇形圆心角的度数；

（4）如果骑共享单车的平均速度为12km/h，请估算，在租用共享单车的市民中，骑车路程不超过6km的人数所占的百分比．

【题目】如图，在平面直角坐标系xOy中，一次函数y=3x的图象与反比例函数的图象的一个交点为A（1，m）．

（1）求反比例函数的解析式；

（2）若点P在直线OA上，且满足PA=2OA，直接写出点P的坐标．

【题目】已知如图，在△ABC中，AB=BC=4，∠ABC=90°，M是AC的中点，点N在AB上（不同于A、B），将△ANM绕点M逆时针旋转90°得△A1PM.

（1）画出△A1PM

（2）设AN=x，四边形NMCP的面积为y，直接写出y关于x的函数关系式，并求y的最大或最小值．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网