��Ŀ����
����Ŀ�����������֣�
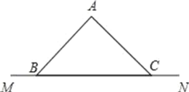
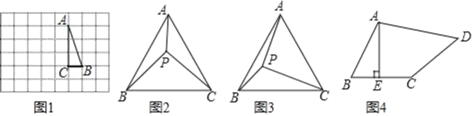
��1����ͼ1���ڱ߳�Ϊ1����λ���ȵ�С��������ɵ������У���ABC������������ڸ���ϣ��밴Ҫ��ͼ����ABC�Ƶ�A˳ʱ�뷽����ת90������B�Ķ�Ӧ��ΪB������C�Ķ�Ӧ��ΪC��������BB������ʱ��ABB�����ڶ��ٶȣ�
����������
��ij����ѧ��ȤС���У�С��ͬѧ�������������⣺
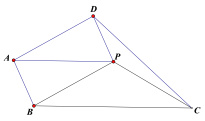
��2����ͼ2���ڵȱ���ABC�У���P���ڲ�����PA��3��PC��4����APC��150������PB�ij���
����ͬѧ�ǵĹ۲졢������˼���������������������γ��������뷨������APC�Ƶ�A��˳ʱ�뷽����ת60�����õ���ABP��������PP����Ѱ��PA��PB��PC����֮���������ϵ������ο����ǵ��뷨����ɸ�����Ľ����̣�
��ѧ�����ã�
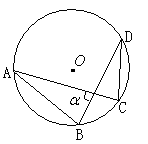
��3����ͼ3���ڵȱ���ABC�У�AC��7����P����ABC�ڣ��ҡ�APC��90������BPC��120��������APC�������
��˼ά��չ��
��ͼ4�����ı���ABCD�У�AE��BC������ΪE����BAE����ADC��BE��CE��1��CD��3��AD��kAB��kΪ����������ֱ��д��BD�ij����ú�k��ʽ�ӱ�ʾ����
���𰸡����������֡���1����AB��B��45�㣻������������2��PB��5����ѧ�����á���3��S��APC��7![]() ����˼ά��չ��BD��
����˼ά��չ��BD��![]() ��
��
��������
��1������BB�䣬����ABC�Ƶ�A��˳ʱ�뷽����ת90�㣬��AB��AB�䣬��B��AB��90�㣬���ɵó��𰸣�
��2���ɡ�ABC��60�㣬����APC�Ƶ�A��˳ʱ�뷽����ת60�㣬�õ���ABP'������PP�䣬���APP���ǵȱ������Σ���APC����AP��B��150�㣬PC��P��B��4���ó���AP��P��60�㣬P��P��AP��3����PP��B��90�㣬�ɹ��ɶ������ɵó������
��3������APB�Ƶ�A����ʱ�뷽����ת60�㣬�õ���AP��C�䣬����PP�䣬���APP���ǵȱ������Σ���AP��C����APB��360��90��120�㣽150�㣬�ó�PP�䣽AP����AP��P����APP�䣽60�㣬��PP��C��90�㣬��P��PC��30�㣬�Ƴ�PP�䣽![]() PC����AP��
PC����AP��![]() PC���ɹ��ɶ����ó�AP2��PC2��AC2������
PC���ɹ��ɶ����ó�AP2��PC2��AC2������![]() PC��2��PC2��72�����PC��2
PC��2��PC2��72�����PC��2![]() ��AP��
��AP��![]() ���������������ʽ���ɵó������
���������������ʽ���ɵó������
��4���ɵ��������ε����ʵó�AB��AC������ABD�Ƶ�A��ʱ����ת�õ���ACG������DG����BD��CG���ó���BAC����DAG����ABC����ACB����ADG����AGD��֤����ABC�ס�ADG���ó�BC��2��DG��kBC��2k��֤�á�GDC��90�㣬�ó�CG��![]() �����ɵó������
�����ɵó������
�⣺��1������BB��������ABC�Ƶ�A��˳ʱ�뷽����ת90������ͼ1��ʾ��

��AB��AB������B��AB��90����
���AB��B��45����
�ʴ�Ϊ��45����
��2���ߡ�ABC�ǵȱ������Σ�
���ABC��60����
����APC�Ƶ�A��˳ʱ�뷽����ת60�����õ���ABP'������PP������ͼ2��ʾ��
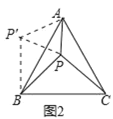
����APP���ǵȱ������Σ���APC����AP��B��150����PC��P��B��4��
���AP��P
���PP��B��90����
��PB��![]() ��
��
��3������APB�Ƶ�A����ʱ�뷽����ת60�����õ���AP��C������PP������ͼ3��ʾ��
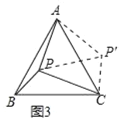
����APP���ǵȱ������Σ���AP��C����APB��360����90����120����150����
��PP����AP����AP��P����APP����60����
���PP��C��90������P��PC��30����
��PP����![]() PC����AP��
PC����AP��![]() PC��
PC��
�ߡ�APC��90����
��AP2+PC2��AC2������![]() PC��2+PC2��72��
PC��2+PC2��72��
��PC��2![]() ��
��
��AP��![]() ��
��
��S��APC��![]() APPC��
APPC��![]() ��
��![]() ��2
��2![]() ��7
��7![]() ��
��
(4)��AE��BC��BE��EC��
��AB��AC������ABD�Ƶ�A��ʱ����ת�õ���ACG������DG����BD��CG����ͼ4��ʾ��
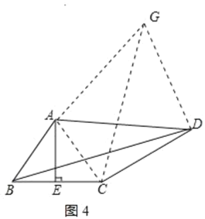
�ߡ�BAD����CAG��
���BAC����DAG��
��AB��AC��AD��AG��
���ABC����ACB����ADG����AGD��
���ABC�ס�ADG��
��AD��kAB��BE��CE��1��
��BC��2��DG��kBC��2k��
�ߡ�BAE+��ABC��90������BAE����ADC��
���ADG+��ADC��90����
���GDC��90����
��CG��![]() ��
��
��D��CG��![]() ��
��