题目内容
【题目】以长为2的线段为边作正方形ABCD，取AB的中点P，连接PD，在BA的延长线上取点F，使PF＝PD，以AF为边作正方形AMEF，点M在AD上，如图所示．
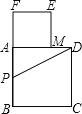
（1）求AM、DM的长；
（2）求证：AM2＝ADDM．
【答案】（1）AM＝
﹣1，DM＝3﹣；（2）见解析.
【解析】
（1）根据勾股定理可求得PD的长，进一步即可求得AF的长，亦即AM的长，而DM=AD－AM，问题即得解决；
（2）根据（1）中求得的数据分别计算AM2与ADDM，即可证明.
（1）解：在Rt△APD中，PA＝
AB＝1，AD＝2，
∴PD＝
，
∴AM＝AF＝PF﹣PA＝PD﹣PA＝﹣1，
DM＝AD﹣AM＝2﹣(﹣1)＝3﹣；
（2）证明：∵AM2＝（﹣1）2＝6﹣2，ADDM＝2（3﹣）＝6﹣2，
∴AM2＝ADDM．
练习册系列答案
相关题目
