题目内容
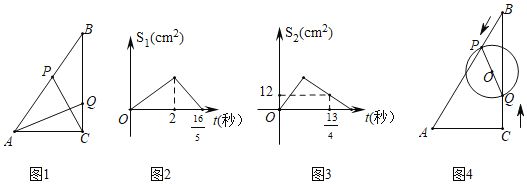
【题目】如图,矩形AOBC的顶点坐标分别为A(0,3),O(0,0),B(4,0),C(4,3),动点F在边BC上(不与B.C重合),过点F的反比例函数y=![]() 的图象与边AC交于点E,直线EF分别与y轴和x轴相交于点D和G.给出下列命题:①若k=4,则△OEF的面积为
的图象与边AC交于点E,直线EF分别与y轴和x轴相交于点D和G.给出下列命题:①若k=4,则△OEF的面积为![]() ;②若k=
;②若k=![]() ,则点C关于直线EF的对称点在x轴上;③满足题设的k的取值范围是0<k≤12;④若DEEG=
,则点C关于直线EF的对称点在x轴上;③满足题设的k的取值范围是0<k≤12;④若DEEG=![]() ,则k=1.其中正确的命题的序号是____________(填序号).
,则k=1.其中正确的命题的序号是____________(填序号).
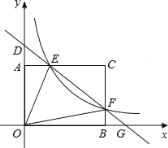
【答案】②④
【解析】
(1)若k=4,则计算![]() ,故命题①错误;
,故命题①错误;
(2)如答图所示,若k=![]() ,可证明直线EF是线段CN的垂直平分线,故命题②正确;
,可证明直线EF是线段CN的垂直平分线,故命题②正确;
(3)因为点F不经过点C(4,3),所以k≠12,故命题③错误;
(4)求出直线EF的解析式,得到点D、G的坐标,然后求出线段DE、EG的长度;利用算式DEEG=![]() ,求出k=1,故命题④正确.
,求出k=1,故命题④正确.
命题①错误,理由如下:
∵k=4,
∴![]()
∴![]()
∴S△OEF=S矩形AOBCS△AOES△BOFS△CEF
=S矩形AOBC![]() ,
,
![]()
![]()
![]()
∴![]() ,故命题①错误;
,故命题①错误;
命题②正确,理由如下:
∵![]()
∴![]()
∴![]()
如答图,过点E作EM⊥x轴于点M,则EM=3,OM=![]() ;
;
在线段BM上取一点N,使得EN=CE=![]() ,连接NF.
,连接NF.
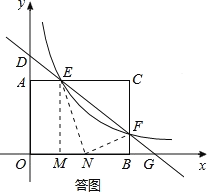
在Rt△EMN中,由勾股定理得:![]()
∴![]()
在Rt△BFN中,由勾股定理得:![]()
∴NF=CF,
又∵EN=CE,
∴直线EF为线段CN的垂直平分线,即点N与点C关于直线EF对称,
故命题②正确;
命题③错误,理由如下:
由题意,点F与点C(4,3)不重合,所以k≠4×3=12,故命题③错误;
命题④正确;理由如下:
为简化计算,不妨设k=12m,
设直线EF的解析式为y=ax+b,则有
![]() 解得
解得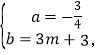
∴![]()
令x=0,得y=3m+3,∴D(0,3m+3);
令y=0,得x=4m+4,∴G(4m+4,0).
如答图,过点E作EM⊥x轴于点M,则OM=AE=4m,EM=3.
在Rt△ADE中,AD=ODOA=3m,AE=4m,由勾股定理得:DE=5m;
在Rt△MEG中,MG=OGOM=(4m+4)4m=4,EM=3,由勾股定理得:EG=5.
∴DEEG=5m×5=25m=![]() ,解得
,解得![]() ,
,
∴k=12m=1,故命题④正确,
综上所述,正确的命题是:②④,
故答案为:②④.

【题目】某乒乓球馆使用发球机进行辅助训练,出球口在桌面中线端点A处的正上方,如果每次发出的乒乓球的运动路线固定不变,且落在中线上,在乒乓球从发射出到第一次落在桌面的运行过程中,设乒乓球与端点A的水平距离为x(米),距桌面的高度为y(米),运行时间为t(秒),经多次测试后,得到如下部分数据:
t(秒) | 0 | 0.16 | 0.2 | 0.4 | 0.6 | 0.64 | 0.8 | … |
x(米) | 0 | 0.4 | 0.5 | 1 | 1.5 | 1.6 | 2 | … |
y(米) | 0.25 | 0.378 | 0.4 | 0.45 | 0.4 | 0.378 | 0.25 | … |
(1)如果y是t的函数,
①如图,在平面直角坐标系tOy中,描出了上表中y与t各对对应值为坐标的点.请你根据描出的点,画出该函数的图象;
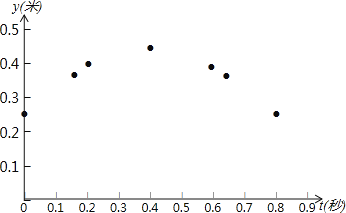
②当t为何值时,乒乓球达到最大高度?
(2)如果y是关于x的二次函数,那么乒乓球第一次落在桌面时,与端点A的水平距离是多少?