题目内容
如图,Rt△AOB中,∠OAB=90°,以O为坐标原点,OA所在的直线为x轴建立平面直角坐标系,将△OAB沿OB折叠后,点A落在第一象限的点C处,已知B点坐标是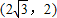 ;一个二次函数的图象经过O、C、A三个点.
;一个二次函数的图象经过O、C、A三个点.(1)求此二次函数的解析式;
(2)直线OC上是否存在点Q,使得△AQB的周长最小?若存在请求出Q点的坐标,若不存在请说明理由;
(3)若抛物线的对称轴交OB于点D,设P为线段DB上一点,过P点作PM∥y轴交抛物线于点M,问:是否存在这样的点P,使得四边形CDPM为等腰梯形?若存在请求出P点坐标,若不存在请说明理由.
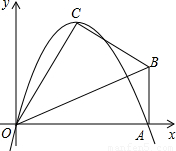
【答案】分析:(1)在Rt△AOB中,根据AB的长和∠BOA的度数,可求得OA的长,根据折叠的性质即可得到OA=OC,且∠BOC=∠BOA=30°,过C作CD⊥x轴于D,即可根据∠COD的度数和OC的长求得CD、OD的值,从而求出点C的坐标.将A、C的坐标代入抛物线的解析式中,通过联立方程组即可求出待定系数的值,从而确定该抛物线的解析式;
(2)作出A关于OC的对称点,连接AA′,与OC的交点就是所求的点,求出OC与AA′的解析式,解方程组即可;
(3)根据(2)所得抛物线的解析式可得到其顶点的坐标(即C点),设直线MP与x轴的交点为N,且PN=t,在Rt△OPN中,根据∠PON的度数,易得PN、ON的长,即可得到点P的坐标,然后根据点P的横坐标和抛物线的解析式可求得M点的纵坐标,过M作ME⊥CD(即抛物线对称轴)于E,过P作PQ⊥CD于Q,若四边形CDPM是等腰梯形,那么CE=QD,根据C、M、P、D四点纵坐标,易求得CE、QD的长,联立两式即可求出此时t的值,从而求得点P的坐标.
解答:解:(1)过点C作CH⊥x轴,垂足为H;
∵在Rt△OAB中,∠OAB=90°,∠BOA=30°,AB=2,
∴OB=4,OA=2 ;
;
由折叠的性质知:∠COB=30°,OC=AO=2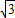 ,
,
∴∠COH=60°,OH= ,CH=3;
,CH=3;
∴C点坐标为( ,3).
,3).
∵抛物线y=ax2+bx(a≠0)经过C(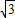 ,3)、A(2
,3)、A(2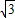 ,0)两点,
,0)两点,
∴ ,
,
解得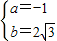 ;
;
∴此抛物线的函数关系式为:y=-x2+2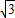 x.
x.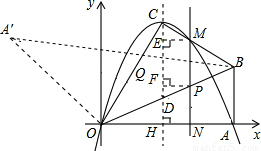
(2)作A关于OC的对称点A′,BA′交OC于点Q.
∵B点坐标是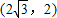
∴tan∠BOA=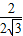 =
=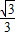
∴∠BOA=30°
∴∠BOC=30°,
∴∠A′OC=∠AOC=∠AOB+∠BOC=60°,
∴OA′与y轴的夹角是30°.
又∵OA=OA′=2 ,
,
∴A′的坐标是:(- ,3)
,3)
设直线A′B的解析式是y=kx+b
根据题意得:
则直线A′B的解析式是y=-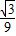 x+
x+ .
.
直线OC的解析式是:y=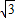 x.
x.
解方程组: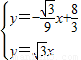 解得:
解得:
故Q的坐标是:( ,
, ).
).
(3)存在.
因为y=-x2+2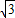 x的顶点坐标为(
x的顶点坐标为( 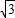 ,3),
,3),
即为点C,MP⊥x轴,垂足为N,设PN=t;
因为∠BOA=30°,
所以ON=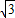 t,
t,
∴P( t,t);
t,t);
作PF⊥CD,垂足为F,ME⊥CD,垂足为E;
把x= t代入y=-x2+2
t代入y=-x2+2  x,
x,
得y=-3t2+6t,
∴M(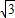 t,-3t2+6t),E(
t,-3t2+6t),E(  ,-3t2+6t),
,-3t2+6t),
同理:F( ,t),D(
,t),D( 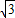 ,1);
,1);
要使四边形CDPM为等腰梯形,只需CE=FD,
即3-(-3t2+6t)=t-1,
解得t= ,t=1(舍),
,t=1(舍),
∴P点坐标为(
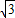 ,
, ),
),
∴存在满足条件的P点,使得四边形CDPM为等腰梯形,此时P点坐标为(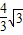 ,
, ).
).
点评:此题主要考查了图形的旋转变化、解直角三角形、二次函数解析式的确定、等腰梯形的判定和性质等重要知识点,难度较大
(2)作出A关于OC的对称点,连接AA′,与OC的交点就是所求的点,求出OC与AA′的解析式,解方程组即可;
(3)根据(2)所得抛物线的解析式可得到其顶点的坐标(即C点),设直线MP与x轴的交点为N,且PN=t,在Rt△OPN中,根据∠PON的度数,易得PN、ON的长,即可得到点P的坐标,然后根据点P的横坐标和抛物线的解析式可求得M点的纵坐标,过M作ME⊥CD(即抛物线对称轴)于E,过P作PQ⊥CD于Q,若四边形CDPM是等腰梯形,那么CE=QD,根据C、M、P、D四点纵坐标,易求得CE、QD的长,联立两式即可求出此时t的值,从而求得点P的坐标.
解答:解:(1)过点C作CH⊥x轴,垂足为H;
∵在Rt△OAB中,∠OAB=90°,∠BOA=30°,AB=2,
∴OB=4,OA=2
 ;
;由折叠的性质知:∠COB=30°,OC=AO=2
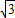 ,
,∴∠COH=60°,OH=
 ,CH=3;
,CH=3;∴C点坐标为(
 ,3).
,3).∵抛物线y=ax2+bx(a≠0)经过C(
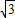 ,3)、A(2
,3)、A(2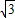 ,0)两点,
,0)两点,∴
 ,
,解得
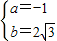 ;
;∴此抛物线的函数关系式为:y=-x2+2
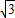 x.
x.
(2)作A关于OC的对称点A′,BA′交OC于点Q.
∵B点坐标是
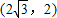
∴tan∠BOA=
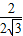 =
=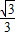
∴∠BOA=30°
∴∠BOC=30°,
∴∠A′OC=∠AOC=∠AOB+∠BOC=60°,
∴OA′与y轴的夹角是30°.
又∵OA=OA′=2
 ,
,∴A′的坐标是:(-
 ,3)
,3)设直线A′B的解析式是y=kx+b
根据题意得:

则直线A′B的解析式是y=-
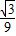 x+
x+ .
.直线OC的解析式是:y=
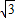 x.
x.解方程组:
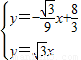 解得:
解得:
故Q的坐标是:(
 ,
, ).
).(3)存在.
因为y=-x2+2
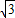 x的顶点坐标为(
x的顶点坐标为( 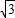 ,3),
,3),即为点C,MP⊥x轴,垂足为N,设PN=t;
因为∠BOA=30°,
所以ON=
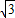 t,
t,∴P(
 t,t);
t,t);作PF⊥CD,垂足为F,ME⊥CD,垂足为E;
把x=
 t代入y=-x2+2
t代入y=-x2+2  x,
x,得y=-3t2+6t,
∴M(
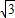 t,-3t2+6t),E(
t,-3t2+6t),E(  ,-3t2+6t),
,-3t2+6t),同理:F(
 ,t),D(
,t),D( 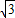 ,1);
,1);要使四边形CDPM为等腰梯形,只需CE=FD,
即3-(-3t2+6t)=t-1,
解得t=
 ,t=1(舍),
,t=1(舍),∴P点坐标为(

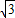 ,
, ),
),∴存在满足条件的P点,使得四边形CDPM为等腰梯形,此时P点坐标为(
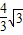 ,
, ).
).点评:此题主要考查了图形的旋转变化、解直角三角形、二次函数解析式的确定、等腰梯形的判定和性质等重要知识点,难度较大

练习册系列答案
相关题目
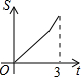
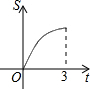
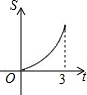
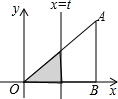 如图,Rt△AOB中,AB⊥OB,且AB=OB=3,设直线x=t截此三角形所得阴影部分的面积为S,则S与t之间的函数关系的图象为下列选项中的( )
如图,Rt△AOB中,AB⊥OB,且AB=OB=3,设直线x=t截此三角形所得阴影部分的面积为S,则S与t之间的函数关系的图象为下列选项中的( )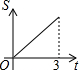
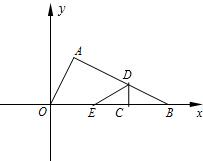 如图在Rt△AOB中,∠BAO=90°,O为坐标原点,B在x轴正半轴上,A在第一象限.OA和AB的长是方程
如图在Rt△AOB中,∠BAO=90°,O为坐标原点,B在x轴正半轴上,A在第一象限.OA和AB的长是方程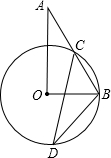 如图,Rt△AOB中,∠AOB=90°,∠A=36°,以OB为半径作⊙O交AB于C,D为优弧BC上一点,求∠BDC的度数.
如图,Rt△AOB中,∠AOB=90°,∠A=36°,以OB为半径作⊙O交AB于C,D为优弧BC上一点,求∠BDC的度数.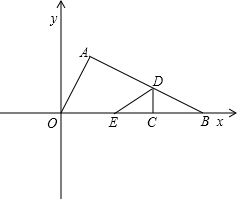 如图在Rt△AOB中,∠BAO=90°,O为坐标原点,B在x轴正半轴上,A在第一象限,OA和AB的长是方程
如图在Rt△AOB中,∠BAO=90°,O为坐标原点,B在x轴正半轴上,A在第一象限,OA和AB的长是方程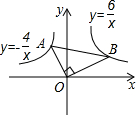 如图,Rt△AOB中∠AOB=90°,点A在y=-
如图,Rt△AOB中∠AOB=90°,点A在y=-