题目内容
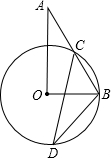 如图,Rt△AOB中,∠AOB=90°,∠A=36°,以OB为半径作⊙O交AB于C,D为优弧BC上一点,求∠BDC的度数.
如图,Rt△AOB中,∠AOB=90°,∠A=36°,以OB为半径作⊙O交AB于C,D为优弧BC上一点,求∠BDC的度数.
分析:连接OC,由∠AOB=90°,∠A=36°,得∠ABO=90°-36°=54°,而OC=OB,则有∠OBC=∠OCB=54°,∠BOC=180°-54°-54°=72°,利用圆周角定理可得∠BDC=
∠BOC.
| 1 |
| 2 |
解答: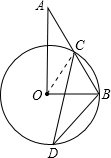 解:连接OC,如图,
解:连接OC,如图,
∵∠AOB=90°,∠A=36°,
∴∠ABO=90°-36°=54°,
OC=OB,则有∠OBC=∠OCB=54°,
∴∠BOC=180°-54°-54°=72°,
∴∠BDC=
∠BOC=36°.
 解:连接OC,如图,
解:连接OC,如图,∵∠AOB=90°,∠A=36°,
∴∠ABO=90°-36°=54°,
OC=OB,则有∠OBC=∠OCB=54°,
∴∠BOC=180°-54°-54°=72°,
∴∠BDC=
| 1 |
| 2 |
点评:本题考查了圆周角定理.在同圆或等圆中,同弧或等弧所对的圆周角相等,一条弧所对的圆周角是它所对的圆心角的一半.也考查了等腰三角形的性质和三角形的内角和定理.

练习册系列答案
相关题目
 如图,Rt△AOB中,AB⊥OB,且AB=OB=3,设直线x=t截此三角形所得阴影部分的面积为S,则S与t之间的函数关系的图象为下列选项中的( )
如图,Rt△AOB中,AB⊥OB,且AB=OB=3,设直线x=t截此三角形所得阴影部分的面积为S,则S与t之间的函数关系的图象为下列选项中的( )


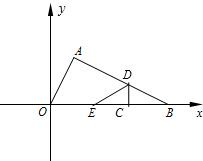 如图在Rt△AOB中,∠BAO=90°,O为坐标原点,B在x轴正半轴上,A在第一象限.OA和AB的长是方程
如图在Rt△AOB中,∠BAO=90°,O为坐标原点,B在x轴正半轴上,A在第一象限.OA和AB的长是方程 如图在Rt△AOB中,∠BAO=90°,O为坐标原点,B在x轴正半轴上,A在第一象限,OA和AB的长是方程
如图在Rt△AOB中,∠BAO=90°,O为坐标原点,B在x轴正半轴上,A在第一象限,OA和AB的长是方程 如图,Rt△AOB中∠AOB=90°,点A在y=-
如图,Rt△AOB中∠AOB=90°,点A在y=-